Bài 3.46 trang 162 SBT hình học 11
Giải bài 3.46 trang 162 sách bài tập hình học 11. Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây: a) AB’ và BC’ b) AC’ và CD’
Đề bài
Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây:
a) AB’ và BC’
b) AC’ và CD’
Lời giải chi tiết
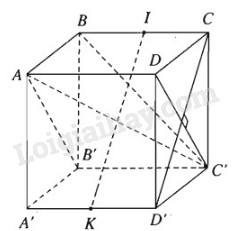
a) Ta có \(AB'\parallel DC'\). Gọi là góc giữa AB’và BC’, khi đó \(\alpha = \widehat {DC'B}\).
Vì tam giác BC’D đều nên \(\alpha = {60^0}\)
b) Gọi \(\beta \) là góc giữa AC’ và CD’.
Vì CD’⊥C’D và CD’⊥AD
( do AD⊥(CDD’C’)
Ta suy ra CD’⊥(ADC’B’)
Vậy CD’⊥AC’ hay \(\beta = {90^0}\)
Chú ý. Ta có thể chứng minh \(\beta = {90^0}\) bằng cách khác như sau:
Gọi I và K lần lượt là trung điểm của các cạnh BC và A’D’. Ta có \(IK\parallel C{\rm{D}}'\). Dễ dàng chứng minh được AIC’K là một hình bình hành có bốn cạnh bằng nhau và đó là một hình thoi. Vậy AC’⊥IK hay AC’⊥CD’ và góc \(\beta = {90^0}\).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.46 trang 162 SBT hình học 11 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.46 trang 162 SBT hình học 11 timdapan.com"







