Giải bài 35 trang 117 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh:

a) CH là tia phân giác của góc ACE;

b) OH // EC.

Lời giải chi tiết

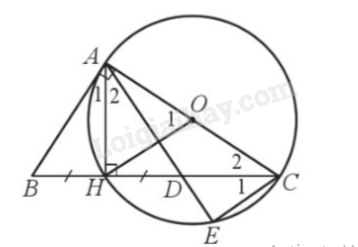
a) Ta có \(\widehat {{A_2}} = \widehat {{C_1}}\) (góc nội tiếp chắn cung HE của (O)).

Xét \(\Delta ABD\)có \(AH \bot BD,BH = DH\), hay AH vừa là đường cao, vừa là đường trung tuyến, nên tam giác ABD cân tại A, do đó AH đồng thời là đường phân giác, suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\).

Vậy \(\widehat {{A_1}} = \widehat {{C_1}}\) (1)

Mặt khác \(\widehat {{A_1}} + \widehat B = 90^\circ \) (do tam giác AHB vuông tại H), \(\widehat {{C_2}} + \widehat B = 90^\circ \) (do tam giác ACB vuông tại A). Do đó  \(\widehat {{A_1}} = \widehat {{C_2}}\) (2)

Từ (1) và (2) suy ra \(\widehat {{C_2}} = \widehat {{C_1}}\) hay CH là tia phân giác của góc ACE.

b) Ta có \(\widehat {{O_1}}\) là góc ở tâm và \(\widehat {{C_2}}\)  là góc nội tiếp cùng chắn cung AH của (O)

nên \(\widehat {{O_1}} = 2\widehat {{C_2}}\)= \(\widehat {ACE}\) = sđ\(\overset\frown{AH}\).

Mà \(\widehat {{O_1}};\widehat {ACE}\) là 2 góc đồng vị nên OH // EC.