Bài 3.33 trang 160 SBT hình học 11

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng khoảng cách từ các điểm A’, B, D; C, B’, D tới đường chéo AC’ bằng nhau. Tính khoảng cách đó.

Lời giải chi tiết

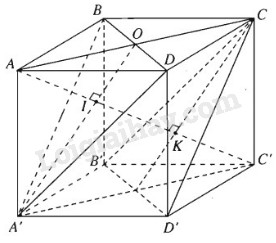
Điểm A cách đều ba đỉnh của tam giác đều A’BD vì ta có \(AB = A{\rm{D}} = AA' = a\), điểm C’ cũng cách đều ba đỉnh của tam giác đều đó vì ta có: 

\(C'B = C'D = C'A' = a\sqrt 2 \)

Vậy AC’ là trục của đường tròn ngoại tiếp tam giác A’BD, tức là đường thẳng AC’ vuông góc với mặt phẳng (A’BD) tại trọng tâm I của tam giác A’BD. Ta cần tìm khoảng cách A’I.

Ta có \(A'I = BI = DI = {2 \over 3}A'O\) với O là tâm của hình vuông ABCD

Ta lại có \(AO' = B{\rm{D}}{{\sqrt 3 } \over 2}\)

\( = a\sqrt 2 .{{\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\)

Vậy \(A'I = {2 \over 3}A'O = {2 \over 3}.{{a\sqrt 6 } \over 2} = {{a\sqrt 6 } \over 3}\)

Tương tự điểm C’ cách đều ba đỉnh của tam giác đều CB’D’, tính được khoảng cách từ C, B’, D’ tới đường chéo AC’.