Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1
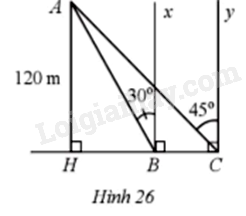
Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là \(\widehat {ABx} = 30^\circ ,\widehat {ACx} = 45^\circ \) (hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).
Đề bài
Flycam là từ viết tắt của Fly camera. Đây là thiết bị bay không người lái có lắp camera hay máy ảnh để quay phim hoặc chụp ảnh từ trên cao. Một chiếc Flycam đang ở vị trí A cách cây cầu BC (theo phương thẳng đứng) một khoảng AH = 120m. Biết góc tạo bởi phương AB, AC với các phương vuông góc với mặt cầu tại B, C lần lượt là \(\widehat {ABx} = 30^\circ ,\widehat {ACx} = 45^\circ \) (hình 26). Tính độ dài BC của cây cầu (làm tròn kết quả đến hàng phần trăm của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng tỉ số lượng giác trong các tam giác vuông AHB và AHC để tính HB, HC.
Bước 2: \(BC = HC - HB\).
Lời giải chi tiết
Ta có \(AH \bot HC,Bx \bot HC,Cy \bot HC\) nên \(AH//Bx//Cy\).
Suy ra \(\widehat {ABx} = \widehat {HAB} = 30^\circ ,\widehat {ACx} = \widehat {CAH} = 45^\circ \) (các cặp góc so le trong).
Xét tam giác ABH vuông tại H, ta có \(\tan \widehat {HAB} = \frac{{BH}}{{AH}}\) hay \(BH = AH.\tan \widehat {HAB} = 120.\tan 30^\circ = 40\sqrt 3 \)m.
Xét tam giác ACH vuông tại H, ta có \(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(BH = CH.\tan \widehat {HAC} = 120.\tan 45^\circ = 120\)m.
Ta lại có \(BC = HC - HB = 120 - 40\sqrt 3 \approx 50,72\)m.
Vậy chiều dài của cây cầu khoảng 50,72m.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 26 trang 89 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"







