Giải bài 24 trang 89 sách bài tập toán 9 - Cánh diều tập 1
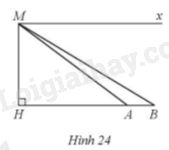
Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là \(\widehat {AMx} = 37^\circ ,\widehat {BMx} = 31^\circ \)với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Đề bài
Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là \(\widehat {AMx} = 37^\circ ,\widehat {BMx} = 31^\circ \)với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải - Xem chi tiết
Bước 1: Áp dụng tỉ số lượng giác trong 2 tam giác HMA và HMB để tính HA, HB.
Bước 2: \(AB = HB - HA\).
Lời giải chi tiết
Do Mx // AB nên \(\widehat {AMx} = \widehat {MAH} = 37^\circ \), \(\widehat {BMx} = \widehat {MBH} = 31^\circ \) (các cặp góc so le trong).
Xét tam giác MAH vuông tại H ta có:
\(\tan \widehat {MAH} = \frac{{MH}}{{AH}}\) hay \(AH = \frac{{MH}}{{\tan \widehat {MAH}}} = \frac{{920}}{{\tan 37^\circ }}\)
Xét tam giác MBH vuông tại H ta có:
\(\tan \widehat {MBH} = \frac{{MH}}{{BH}}\) hay \(BH = \frac{{MH}}{{\tan \widehat {MBH}}} = \frac{{920}}{{\tan 31^\circ }}\)
Độ dài AB của cây cầu là:
\(AB = HB - HA = \frac{{920}}{{\tan 31^\circ }} - \frac{{920}}{{\tan 37^\circ }} \approx 310\)m.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 24 trang 89 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"







