Bài 22 trang 158 SBT toán 8 tập 1
Giải bài 22 trang 158 sách bài tập toán 8. Cho hình bình hành ABCD (h. 184). Đường phân giác của các góc A và C cắt đường chéo BD tai E, F. Chứng minh rằng hai hình ABCFE và ADCFE có cùng diện tích.
Đề bài
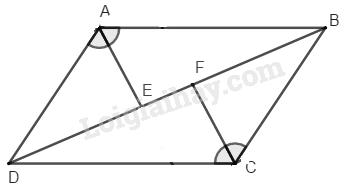
Cho hình bình hành \(ABCD\) \((h. 184).\) Đường phân giác của các góc \(A\) và \(C\) cắt đường chéo \(BD\) tại \(E, \,F.\)
a) Chứng minh rằng hai hình \(ABCFE\) và \(ADCFE\) có cùng diện tích.
b) Các hình đó có phải đa giác lồi không? Vì sao?
Phương pháp giải - Xem chi tiết
a) Chứng minh \({S_{ABE}} = {S_{CDF}}\)
\( {S_{AED}} = {S_{CFB}}\)
Từ đó suy ra: \({S_{ABCFE}} = {S_{ADCFE}}\)
b) Định nghĩa: Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.
Lời giải chi tiết
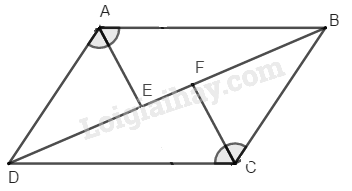
Xét \(∆ ABE\) và \(∆ CDF\) có:
\(\widehat A = \widehat C\) (gt)
\(AB=CD\) (vì \(ABCD\) là hình bình hành)
\(\widehat B = \widehat D\) (vì \(ABCD\) là hình bình hành)
\(\Rightarrow ∆ ABE = ∆ CDF \,(g.c.g)\)
\( \Rightarrow {S_{ABE}} = {S_{CDF}}\) \((1)\)
Xét \(∆ AED\) và \(∆ CFB\) có:
\(\widehat A = \widehat C\) (gt)
\(AD=CB\) (vì \(ABCD\) là hình bình hành)
\(\widehat D = \widehat B\) (vì \(ABCD\) là hình bình hành)
\(\Rightarrow∆ AED = ∆ CFB \,(g.c.g)\)
\( \Rightarrow {S_{AED}} = {S_{CFB}}\) \((2)\)
Từ \((1)\) và \((2)\) suy ra:
\({S_{ABE}} + {S_{CFB}} = {S_{CDF}} + {S_{AED}}\)
Hay \({S_{ABCFE}} = {S_{ADCFE}}\)
b. Hình \(ABCFE\) không phải đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh \(EF.\)
Hình \(ADCFE\) không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh \(EF.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 22 trang 158 SBT toán 8 tập 1 timdapan.com"







