Bài 2.19 trang 61 SBT hình học 12
Giải bài 2.19 trang 61 sách bài tập hình học 12. Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
Đề bài
Chứng minh rằng nếu có một mặt cầu tiếp xúc với 6 cạnh của một hình tứ diện thì hình tứ diện đó có tổng các cặp cạnh đối diện bằng nhau.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tiếp tuyến cắt nhau của mặt cầu.
Lời giải chi tiết
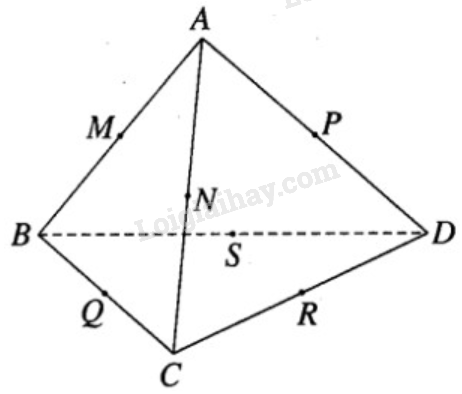
Giả sử có một mặt cầu tiếp xúc với các cạnh AB, AC, AD, BC, CD, BD của tứ diện ABCD lần lượt tại M, N, P, Q, R, S. Khi đó AM, AN, AP là các tiếp tuyến cùng xuất phát từ A nên AM = AN = AP.
Lập luận tương tự ta có: BM = BQ = BS ; CQ = CR = CN ; DR = DS = DP
Vậy AB + CD = AM + MB + CR + RD = AN + BS + CN + DS
= AN + NC + BS + SD = AC + BD
Bằng lí luận tương tự ta chứng minh được AB + CD = AC + BD = AD + BC
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.19 trang 61 SBT hình học 12 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.19 trang 61 SBT hình học 12 timdapan.com"







