Bài 18 trang 198 SBT toán 9 tập 2
Giải bài 18 trang 198 sách bài tập toán 9. Quay tam giác vuông ABC (góc A = 90^o) một vòng quanh cạnh AB là được một hình nón ...
Đề bài
Quay tam giác vuông \(ABC\) \(\left( {\widehat A = {{90}^o}} \right)\) một vòng quanh cạnh \(AB\) là được một hình nón. Tính thể tích và diện tích xung quanh của hình nón biết \(BC=12\,cm\) và \(\widehat {ABC} = {30^o}.\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức:
- Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\).
- Thể tích hình nón: \(\displaystyle V = {1 \over 3}\pi {r^2}h\).
(\(r\) là bán kính đường tròn đáy, \( l\) là đường sinh, \(h\) là chiều cao).
Lời giải chi tiết
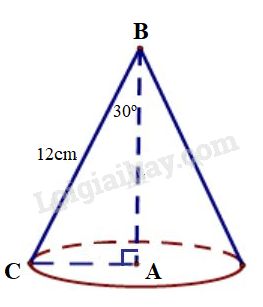
Xét \(\Delta ABC\) vuông tại \(A\), ta có:
\(AB = BC.\cos B = BC.\cos {30^o} \)\(\,= 12.\dfrac{{\sqrt 3 }}{2} = 6\sqrt 3 \,\left( {cm} \right).\)
\(AC = BC.\sin B = BC.\sin {30^o} \)\(\,= 12.\dfrac{1}{2} = 6\,\left( {cm} \right).\)
Quay tam giác vuông \(ABC\) một vòng quanh cạnh \(AB\) ta được một hình nón có chiều cao \(AB,\) bán kính đường tròn đáy là \(AC\) và đường sinh \(BC.\)
Diện tích xung quanh của hình nón tạo thành là:
\({S_{xq}} = \pi .AC.BC = \pi .6.12 \)\(\,= 72\pi \,\left( {c{m^2}} \right).\)
Thể tích của hình nón tạo thành là:
\(V = \dfrac{1}{3}.\pi .A{C^2}.AB = \dfrac{1}{3}.\pi {.6^2}.6\sqrt 3 \)\(\,= 72\sqrt 3 \pi \,\left( {c{m^3}} \right).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 198 SBT toán 9 tập 2 timdapan.com"







