Bài 12 trang 197 SBT toán 9 tập 2

Đề bài

Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O)\). Trên đường chéo \(BD\) lấy điểm \(E\) sao cho \(\widehat {DAE} = \widehat {BAC}\). Chứng minh:

a) \(\,\Delta ADE \backsim \Delta ACB,\)\(\,\Delta ABE \backsim \Delta ACD;\)

b) \(\,AD.BC + AB.CD = AC.BD.\)

Lời giải chi tiết

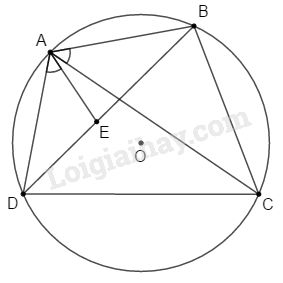
a) Xét \(\,\Delta ADE \) và \( \Delta ACB\) có:

\( \widehat {ADE} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung nhỏ \(AB\))

\(\widehat {DAE} = \widehat {CAB}\) (gt)

\( \Rightarrow \,\Delta ADE \backsim \Delta ACB\) (g.g)

Ta có:

\(\begin{array}{l}
\widehat {BAE} = \widehat {BAC} + \widehat {CAE}\\
\widehat {CAD} = \widehat {DAE} + \widehat {CAE}
\end{array}\)

Mà \(\widehat {BAC} = \widehat {DAE}\) (gt) nên \(\widehat {BAE} = \widehat {CAD}\)

Xét \(\Delta ABE \) và \( \Delta ACD\) có:

\(\widehat {BAE} = \widehat {CAD}\) (chứng minh trên)

\(\widehat {ABE} = \widehat {ACD}\) (hai góc nội tiếp cùng chắn cung nhỏ \(AD\))

\( \Rightarrow \,\Delta ABE \backsim \Delta ACD\) (g.g).

b) Vì \(\Delta ADE \backsim \Delta ACB\) (câu a) suy ra \(\dfrac{{AD}}{{AC}} = \dfrac{{DE}}{{CB}}\)

\(\Rightarrow AD.CB = AC.DE\)     (1)

Vì \(\Delta ABE \backsim \Delta ACD\) (câu a) suy ra \(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CD}}\)

\(\Rightarrow AB.CD = AC.BE\)     (2)

Từ (1) và (2) ta có:

\(AD.CB + AB.CD\)\(\, = AC.DE + AC.BE\)\(\, = AC.\left( {DE + BE} \right) = AC.BD.\)

Vậy \(\,AD.BC + AB.CD = AC.BD.\)