Bài 17 trang 67 SBT toán 7 tập 1

Đề bài

Đố vui: Một kết quả bất ngờ. Biết rằng bán kính Trái Đất \({R_{T{\rm{D}}}} \approx 6370km\) (hình dưới). Giả sử một chiếc vệ tinh bay vòng quanh Trái Đất và cách mặt đất \(100\,km.\)

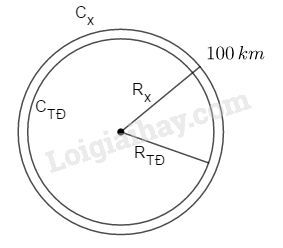
a) Em hãy dự đoán xem quãng đường vệ tinh một vòng dài hơn chu vi Trái Đất khoảng bao nhiêu ki-lô-mét: trên \(1000\,km\) hay dưới \(1000\,km?\)

b) Em hãy tính cụ thể và cho biết kết quả.

Lời giải chi tiết

a) Vì vệ tinh cách mặt đất là \(100\,km\) nên chu vi vệ tinh quay vòng hơn chu vi trái đất một khoảng \(2.3,14.100\) nên nhỏ hơn 1000km

b) Gọi bán kính của Trái Đất \({{\rm{R}}_{T{\rm{D}}}}\), bán kính quỹ đạo vệ tinh \({{\rm{R}}_{VT}}\)

Chu vi trái đất \({\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}\), chu vi quỹ đạo vệ tinh \({\rm{2}}\pi {{\rm{R}}_{VT}}\)

Vì chu vi của đường tròn tỉ lệ thuận với bán kính nên ta có:

\(\eqalign{
& {{{\rm{2}}\pi {{\rm{R}}_{VT}}} \over {{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}}} = {{{{\rm{R}}_{VT}}} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr 
&  \Rightarrow \frac{{{\rm{2}}\pi {{\rm{R}}_{VT}}}}{{{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}}} - 1 = \frac{{{{\rm{R}}_{VT}}}}{{{{\rm{R}}_{T{\rm{D}}}}}} - 1\cr& \Rightarrow {{{\rm{2}}\pi {{\rm{R}}_{VT}} - {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}} \over {{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}}} = {{{{\rm{R}}_{VT}} - {{\rm{R}}_{T{\rm{D}}}}} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr 
& \Rightarrow {\rm{2}}\pi {{\rm{R}}_{VT}} - {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}} = {{{\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}}({{\rm{R}}_{VT}} - {{\rm{R}}_{T{\rm{D}}}})} \over {{{\rm{R}}_{T{\rm{D}}}}}} \cr 
& \Rightarrow {\rm{2}}\pi {{\rm{R}}_{VT}} - {\rm{2}}\pi {{\rm{R}}_{T{\rm{D}}}} = 2\pi .100 \approx 628(km) \cr} \)

Quãng đường vệ tinh bay dài hơn chu vi trái đất khoảng \(628\,km.\)