Bài 1.60 trang 36 SBT giải tích 12

Cho hàm số: \(y = \dfrac{1}{4}{x^3} - \dfrac{3}{2}{x^2} + 5\)

LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

Phương pháp giải:

- Tìm TXĐ.

- Xét sự biến thiên.

+ Tìm các giới hạn tại vô cực.

+ Tìm khoảng đồng biến, nghịch biến.

+ Tìm cực trị (nếu có).

+ Lập bảng biến thiên.

- Vẽ đồ thị hàm số.

Giải chi tiết:

Tập xác định:\(D = \mathbb{R}\),

* Chiều biến thiên:

+) \(\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty \)

+) \(y' = \dfrac{3}{4}{x^2} - 3x\); \(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 4}\end{array}} \right.\)

Hàm số đồng biến trên mỗi khoảng \(( - \infty ;0),(4; + \infty )\).

Hàm số nghịch biến trên khoảng \(\left( {0;4} \right)\).

Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = 5\). Hàm số đạt cực tiểu tại \(x = 4,{y_{CT}} =  - 3\).

Bảng biên thiên:

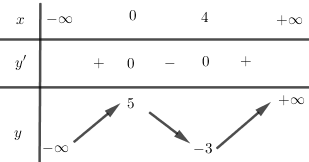
* Đồ thị:

+) Đồ thị đi qua các điểm \(A\left( { - 2; - 3} \right);B\left( {6;5} \right)\) và cắt trục \(Oy\) tại điểm \(\left( {0;5} \right)\).

+) \(y'' = \dfrac{3}{2}x - 3 = 0\) \( \Leftrightarrow x = 2 \Rightarrow y = 1\) suy ra điểm uốn \(U\left( {2;1} \right)\).

+) Vẽ đồ thị:

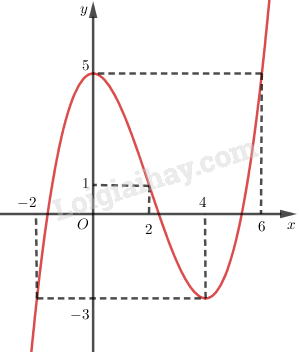
LG b

Tìm các giá trị của tham số \(m\) để phương trình \({x^3}-6{x^2} + m = 0\;\) có \(3\) nghiệm thực phân biệt.

(Đề thi tốt nghiệp THPT năm 2010)

Phương pháp giải:

- Biến đổi phương trình về \(\dfrac{1}{4}{x^3} - \dfrac{3}{2}{x^2} + 5 = 5 - \dfrac{m}{4}\).

- Sử dụng tương quan giữa số nghiệm của phương trình và số giao điểm của đường thẳng \(y = 5 - \dfrac{m}{4}\) với đồ thị hàm số vừa vẽ ở ý a để suy ra kết luận.

Giải chi tiết:

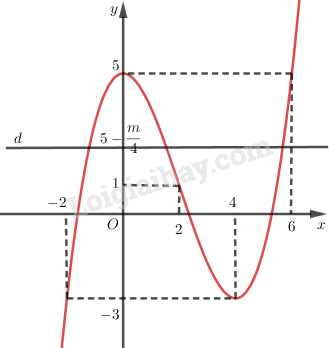
\({x^3} - 6{x^2} + m = 0\)     (1)

\( \Leftrightarrow {x^3} - 6{x^2} =  - m\)\( \Leftrightarrow \dfrac{1}{4}{x^3} - \dfrac{3}{2}{x^2} + 5 = 5 - \dfrac{m}{4}\)

Số nghiệm thực phân biệt của phương trình (1) bằng số giao điểm phân biệt của đồ thị \(\left( C \right)\) và đường thẳng \(\left( d \right):\)\(y = 5 - \dfrac{m}{4}\)

Suy ra \(\left( 1 \right)\) có \(3\) nghiệm thực phân biệt khi và chỉ khi \( - 3 < 5 - \dfrac{m}{4} < 5 \Leftrightarrow 0 < m < 32\).