Bài 1.18 trang 15 SBT giải tích 12

Tìm cực trị của các hàm số sau:

LG a

\(\displaystyle y = {{x + 1} \over {{x^2} + 8}}\)

Giải chi tiết:

TXĐ : R

\(y' = {{{x^2} + 8 - 2x(x + 1)} \over {{{({x^2} + 8)}^2}}} = {{ - {x^2} - 2x + 8} \over {{{({x^2} + 8)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 4 \hfill \cr 
x = 2 \hfill \cr} \right.\)

Bảng biến thiên:

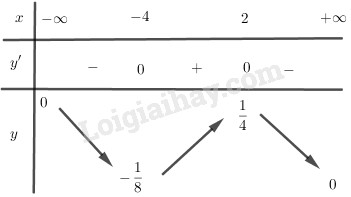
Hàm số đạt cực đại tại \(x = 2\), cực tiểu tại \(x = - 4\) và \({y_{CD}} = y(2) = {1 \over 4};{y_{CT}} = y( - 4) =  - {1 \over 8}\)

LG câu b

\(\displaystyle y = {{{x^2} - 2x + 3} \over {x - 1}}\)

Giải chi tiết:

Hàm số xác định và có đạo hàm với mọi \(x  ≠ 1\).

\(y' = {{{x^2} - 2x - 1} \over {{{(x - 1)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \matrix{
x = 1 - \sqrt 2 \hfill \cr 
x = 1 + \sqrt 2 \hfill \cr} \right.\)

Bảng biến thiên:

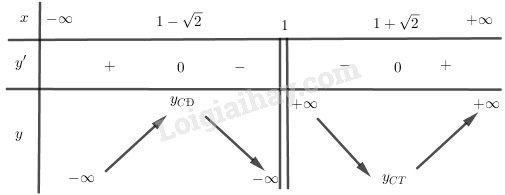
Hàm số đạt cực đại tại \(x = 1 - \sqrt 2 \) và đạt cực tiểu tại \(x = 1 + \sqrt 2\) , ta có:

\({y_{CD}} = y(1 - \sqrt 2 ) =  - 2\sqrt 2 ;\) \({y_{CT}} = y(1 + \sqrt 2 ) = 2\sqrt 2 \).

LG c

\(\displaystyle y = {{{x^2} + x - 5} \over {x + 1}}\)

Giải chi tiết:

TXĐ: R\{-1}

\(y' = {{{x^2} + 2x + 6} \over {{{(x + 1)}^2}}} > 0,\forall x \ne  - 1\)  

Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { -1;+ \infty } \right)\) do đó không có cực trị.

LG d

\(\displaystyle y = {{{{(x - 4)}^2}} \over {{x^2} - 2x + 5}}\)

Giải chi tiết:

\(y = {{{{(x - 4)}^2}} \over {{x^2} - 2x + 5}}\)

Vì \({x^2}-2x + 5>0,\forall x\in R\) nên hàm số xác định trên \(R\).

\(y' = {{2(x - 4)({x^2} - 2x + 5) - {{(x - 4)}^2}(2x - 2)} \over {{{({x^2} - 2x + 5)}^2}}} \) \(= {{2(x - 4)(3x + 1)} \over {{{({x^2} - 2x + 5)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - {1 \over 3} \hfill \cr 
x = 4 \hfill \cr} \right.\)

Bảng biến thiên:

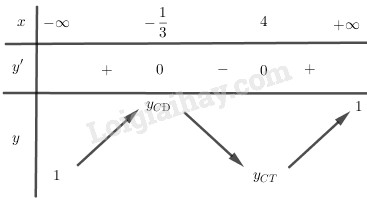
Hàm số đạt cực đại tại \(x =  - {1 \over 3}\) , đạt cực tiểu tại \(x = 4\) và \({y_{CD}} = y( - {1 \over 3}) = {{13} \over 4};{y_{CT}} = y(4) = 0\)