Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 8
Đề bài
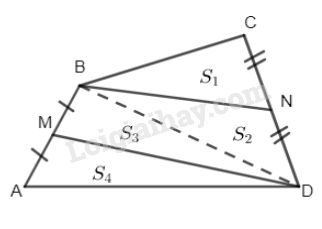
Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD. Chứng minh \({S_{BNDM}} = \dfrac{1}{2}{S_{ABCD}}.\)
Lời giải chi tiết
Nối BD, gọi diện tích các tam giác (theo hình vẽ) là \({S_1},{S_2},{S_3},{S_4}.\) Ta có BN là trung tuyến của \(\Delta BCD\) nên \({S_1} = {S_2}\) (chung đường cao, đáy bằng nhau)
Tương tự \({S_3} = {S_4}\)
\( \Rightarrow {S_2} + {S_3} = {S_1} + {S_4} = {1 \over 2}{S_{ABCD}}\)
Hay \({S_{BNDM}} = {1 \over 2}{S_{ABCD.}}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 8 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 1 - Bài 6 - Chương 2 - Hình học 8 timdapan.com"







