Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 8
Đề bài
Cho hình thang ABCD \(\left( {AB// CD} \right).\) Gọi M, N lần lượt là trung điểm của các cạnh bên AD và BC, kẻ \(MH \bot CD\) (H thuộc CD) và MH cắt đường thẳng ABV tại I, kẻ \(NK \bot CD\) (K thuộc CD) và NK cắt AB tại I
Chứng minh: \({S_{ABCD}} = {S_{HKLI}}.\)
Lời giải chi tiết
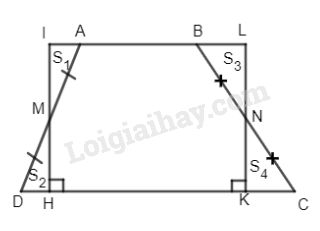
Ta có: \(\Delta AMI = \Delta DMH\) (ch-gn)
\( \Rightarrow {S_1} = {S_2}\) tương tự \({S_3} = {S_4}.\)
\({S_{ABCD}} = {S_2} + {S_{ABNHK}} + {S_4}\)
\({S_{HKLI}} = {S_1} + {S_{ABNHK}} + {S_3}\)
Vậy \({S_{ABCD}} = {S_{HKLI}}.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 8 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 7 - Bài 6 - Chương 2 - Hình học 8 timdapan.com"







