Đề kiểm tra 15 phút - Đề số 5 - Bài 12 - Chương 1 - Hình học 8

Đề bài

Cho hình vuông ABCD. Từ điểm M tùy ý trên đường chéo BD, kẻ ME, MF lần lượt vuông góc với AB và AD. Chứng minh MC = EF  và \(MC \bot {\rm{EF}}\) .

Lời giải chi tiết

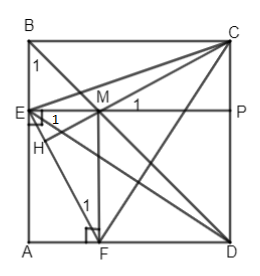
Vẽ \(MP \bot CD.\) Ta có \(MD//AD\) (vì \(AD \bot CD)\)lại có \(ME// AD \Rightarrow MP\) và ME phải trùng nhau (tiên đề Ơ clit) hay ba điểm E, M, P thẳng hàng.

Tứ giác BCPE là hình chữ nhật \( \Rightarrow BE = CP.\)

Mặt khác \(\Delta BEM\) vuông cân (vì \(\widehat {{B_1}} = {45^ \circ }\))

\( \Rightarrow BE = ME\) và M thuộc BD là tia phân giác của góc ADC nên MF = MP.

Do đó hai tam giác vuông \(\Delta EMF = \Delta CPM(c.g.c)\)

\( \Rightarrow EF = MC\) và \(\widehat {{F_1}} = \widehat {{M_1}}.\)

Gọi H là giao điểm của CM và EF ta có \(\widehat {{M_1}} = \widehat {{M_2}}\) (đối đỉnh)

\( \Rightarrow \widehat {{M_2}} = \widehat {{F_1}}\) mà \(\widehat {{F_1}} + \widehat {{E_1}} = {90^ \circ }(\Delta EMF\) vuông )

\( \Rightarrow \widehat {{M_2}} + \widehat {{E_1}} = {90^ \circ } \Rightarrow \widehat {MHE} = {90^ \circ }\) hay \(MC \bot {\rm{EF}}{\rm{.}}\)

Nhận xét:

*Để chứng minh MC = EF, bạn có thể chứng minh MC = MA vì M thuộc BD mà BD là đường trung trực của đoạn AC (tính chất hai đường chéo của hình vuông).

*Ta có thể chứng minh được ba đường sau đây đồng quy CM, BF, DE khi chúng là đường cao của \(\Delta CEF.\)