Đề kiểm tra 15 phút - Đề số 14 - Bài 6 - Chương 2 - Hình học 8

Đề bài

Cho đa giác n – cạnh có diện tích S, các đường thẳng a, b, c cắt nhau tại A, B, C nằm trong tam giác sao cho mỗi đường thẳng chia đa giác thành hai phần có diện tích bằng nhau.

Chứng minh rằng \({S_{ABC}} \le \dfrac{1}{4}S.\)

Lời giải chi tiết

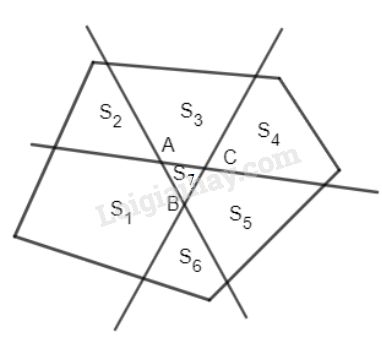
Gọi diện tích của các phần của đa giác được chia bởi các đường thẳng là \({S_1},\,{S_2},{S_3},...\)

Ta có: \({S_1} + {S_2} + {S_6} = \dfrac{1}{2}S = {S_1} + {S_6} + {S_5} + {S_7}\)

\( \Rightarrow {S_2} = {S_5} + {S_7}\) mà \(\dfrac{1 }{ 2}S = {S_1} + {S_2} + {S_3} + {S_7}\)

\( \Rightarrow {1 \over 2}S = {S_1} + {S_5} + {S_7} + {S_3} + {S_7} > 2{S_7}\)

\(\Rightarrow {S_7} < \dfrac{1 }{ 4}S.\)

Vậy \({S_{ABC}} < \dfrac{1 }{4}S\) (đpcm).