Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao
Cho hàm số y = f(x) = 2sin2x
Cho hàm số \(y = f(x) = 2\sin 2x\)
a. Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
b. Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
c. Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
LG a
Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
Ta có \(f(x + kπ) = 2\sin 2(x + kπ) \)
\(= 2\sin (2x + k2π) = 2\sin 2x = f(x),\) \( ∀ x \in\mathbb R\)
LG b
Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
Lời giải chi tiết:
Bảng biến thiên :
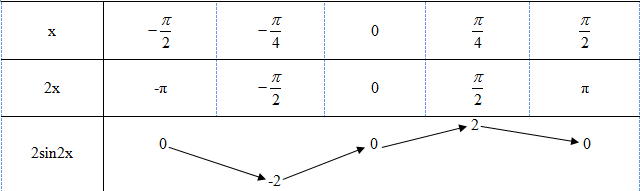
LG c
Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
Lời giải chi tiết:
Đồ thị :
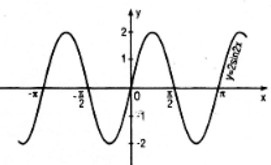
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 6 trang 15 SGK Đại số và Giải tích 11 Nâng cao timdapan.com"







