Bài 1.24 trang 11 SBT Đại số và Giải tích 11 Nâng cao

Biểu diễn nghiệm của mỗi phương trình sau trên đường tròn lượng giác:

LG a

\(\cos 2x = \cos x\)

Lời giải chi tiết:

\(\begin{array}{l}
\cos 2x = \cos x\\
\Leftrightarrow \left[ \begin{array}{l}
2x = x + k2\pi \\
2x = - x + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = k2\pi \\
x = \frac{{k2\pi }}{3}
\end{array} \right.\\
\Leftrightarrow x = \frac{{k2\pi }}{3}
\end{array}\)

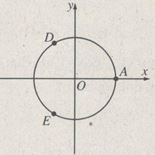
Nghiệm \(x = {{k2\pi } \over 3}\) được biểu diễn bởi ba điểm A, D, E trên hình vẽ:

LG b

\(\sin \left( {{\pi  \over 4} + x} \right) = \sin \left( {2x - {\pi  \over 4}} \right)\)

Lời giải chi tiết:

\(\begin{array}{l}
\sin \left( {\frac{\pi }{4} + x} \right) = \sin \left( {2x - \frac{\pi }{4}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
2x - \frac{\pi }{4} = \frac{\pi }{4} + x + k2\pi \\
2x - \frac{\pi }{4} = \pi - \frac{\pi }{4} - x + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{2} + k2\pi \\
x = \frac{\pi }{3} + \frac{{k2\pi }}{3}
\end{array} \right.
\end{array}\)

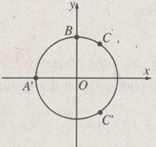
Các nghiệm \(x = {\pi  \over 2} + k2\pi \) và \(x = {\pi  \over 3} + {{k2\pi } \over 3}\) được biểu diễn bởi bốn điểm B, C, A’, C’ trên hình vẽ: