Câu 12 trang 222 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình hộp \(ABC{\rm{D}}.{A_1}{B_1}{C_1}{D_1}\) với M là trung điểm của CD.

a) Xác định giao tuyến của hai mặt phẳng (MAA₁) và (BDD₁B₁).

b) Dựng đường thẳng ∆ qua M cắt BD₁  và AA₁.

c) Gọi P và Q lần lượt là giao điểm của ∆ với BD₁ và AA₁. Tính tỉ số \({{MP} \over {MQ}}\).

d) Xác định thiết diện của hình chóp khi cắt bởi mp(B,∆).

Lời giải chi tiết

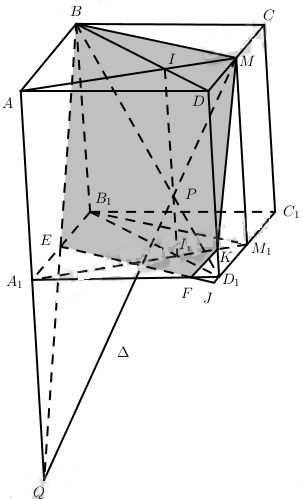
a) Gọi I là giao điểm của AM và BD, M₁ là trung điểm cuae C₁D₁, I₁ là giao điểm của A₁M₁ với B₁D₁. Dễ thấy II₁ chính là giao tuyến của hai mặt phẳng (MAA₁) và (BDD₁B₁).

b) Giả sử đường thẳng ∆ cần tìm cắt BD₁ và AA₁ lần lượt tại P và Q. Khi đó P chính là giao điểm của BD₁ với mp(MAA₁). Vậy P là giao điểm của BD₁ và II₁. Từ đó, suy ra cách dựng đường thẳng ∆ như sau:

- Lấy giao điểm P của BD₁ và II₁.

- Vẽ đường thẳng MP.

Khi đó, đường thẳng MP chính là đường thẳng ∆ cần tìm.

c) Ta có \(DM//AB \Rightarrow {{IM} \over {IA}} = {{M{\rm{D}}} \over {AB}} = {1 \over 2} \Rightarrow {{IM} \over {IA}} = {1 \over 2}\)

và \(IP//AQ \Rightarrow {{MP} \over {PQ}} = {{MI} \over {IA}} = {1 \over 2} \Rightarrow {{MP} \over {PQ}} = {1 \over 2}\)

Suy ra \({{MP} \over {MP + PQ}} = {1 \over {2 + 1}} = {1 \over 3} \Rightarrow {{MP} \over {MQ}} = {1 \over 3}.\)

d) Nối B với Q cắt A₁B₁ tại E. Từ E kẻ EF // B₁M₁ cắt A₁D­₁ tại F. Gọi J là giao điểm của EF với C₁D₁. Nối J với M cắt DD₁ tại K.

Vậy thiết diện là ngũ giác BEFKM.