Bài tập 22 trang 105 Tài liệu dạy – học Toán 8 tập 1
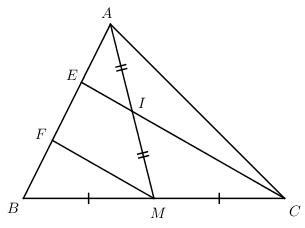
Giải bài tập Cho tam giác nhọn ABC, kẻ trung tuyến AM. Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh rằng:
Đề bài
Cho tam giác nhọn ABC, kẻ trung tuyến AM. Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh rằng:
a) EF = FB;
b) \(AE = {1 \over 3}AB\)
c) CE = 4EI.
Lời giải chi tiết
a) Xét tam giác BEC có : MF // EC (gt)
Và M là trung điểm của BC (gt)
\( \Rightarrow F\) là trung điểm của BE \( \Rightarrow EF = BF\)
b) Xét tam giác AMF có: EI // MF (gt)
Và I là trung điểm của AM (gt)
\( \Rightarrow E\) là trung điểm của AF \( \Rightarrow AE = EF\)
Mà \(EF = BF\) nên \(AE = EF = BF \Rightarrow AE = {1 \over 3}AB\)
c) Xét tam giác EBC ta có :
M là trung điểm của BC (gt) ;
F là trung điểm của BE ;
\( \Rightarrow MF\) là đường trung bình của tam giác EBC \( \Rightarrow MF = {1 \over 2}EC\)
Xét \(\Delta AMF\) ta có:
E là trung điểm của AF (gt);
I là trung điểm của AM (gt) ;
\( \Rightarrow EI\) là đường trung bình của tam giác AMF
\( \Rightarrow EI = {1 \over 2}MF\)
Mà \(MF = {1 \over 2}EC\)
\( \Rightarrow EI = {1 \over 2}.{1 \over 2}EC = {1 \over 4}EC \Rightarrow EC = 4EI\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 22 trang 105 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"