Bài tập 17 trang 104 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC cân tại A, các đường phân giác BD, CE
Đề bài
Cho tam giác ABC cân tại A, các đường phân giác BD, CE \((D \in AC,E \in AB)\) .
a) Chứng minh rằng ED // BC.
b) Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Lời giải chi tiết
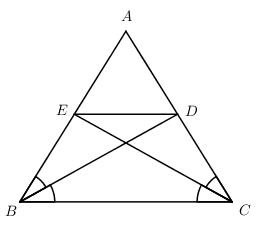
a) Ta có \(\widehat {ABD} = \widehat {DBC} = {{\widehat B} \over 2}\) (BD là tia phân giác của \(\widehat B\))
\(\widehat {ACE} = \widehat {ECB} = {{\widehat C} \over 2}\) (CE là tia phân giác của \(\widehat C\)), \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại A)
Suy ra \(\widehat {ABD} = \widehat {DBC} = \widehat {ACE} = \widehat {ECB}\)
Xét \(\Delta ACE\) và \(\Delta ABD\) ta có :
\(AC = AB\) (\(\Delta ABC\) cân tại A) ;
\(\widehat A\) chung ;
\(\widehat {ACE} = \widehat {ABD}\) (chứng minh trên)
Xét \(\Delta ACE = \Delta ABD\,\,\left( {g.c.g} \right) \Rightarrow AE = AD\) (hai cạnh tương ứng)
\( \Rightarrow \Delta AED\) cân tại A \( \Rightarrow \widehat {AED} = {{{{180}^0} - \widehat A} \over 2}\)
Mà \(\widehat {ABC} = {{{{180}^0} - \widehat A} \over 2}\) (\(\Delta ABC\) cân tại A). Nên \(\widehat {AED} = \widehat {ABC}\)
Mà \(\widehat {AED}\) và \(\widehat {ABC}\) là hai góc đồng vị.
Do đó ED // BC.
b) Vì ED // BC nên tứ giác BEDC là hình thang.
Mà \(\widehat {EBC} = \widehat {DCB}\) (\(\Delta ABC\) cân tại A). Do đó tứ giác BEDC là hình thang cân)
Ta có : \(\widehat {EBD} = \widehat {DBC}\) (hai góc so le trong và ED // BC)
\( \Rightarrow \widehat {EBD} = \widehat {EDB} \Rightarrow \Delta EBD\) cân tại E \( \Rightarrow BE = ED\).
Vậy tứ giác BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 17 trang 104 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"







