Bài tập 11 trang 157 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC nhọn. Gọi D là trung điểm của BC. Trên tia đối của tia DA lấy điểm E sao cho DE = DA.

a) Chứng minh rằng AB // EC.

b) Kẻ AH và EK cùng vuông góc với BC \((H \in BC,K \in BC)\)  . Chứng minh rằng AH = EK.

c) Trên AC lấy điểm M, trên BE lấy điểm N sao cho AM = EN. Chứng minh rằng ba điểm M, D, N thẳng hàng.

Lời giải chi tiết

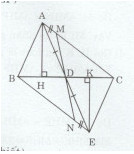
a)Xét tam giác ABD và ECD có:

BD = CD (D là trung điểm của BC)

\(\widehat {BDA} = \widehat {CDE}\)   (hai góc đối đỉnh)

AD = ED (giả thiết)

Do đó: \(\Delta ABD = \Delta ECD(c.g.c) \Rightarrow \widehat {ABD} = \widehat {ECD}\)

Mà \(\widehat {ABD}\)   và  \(\widehat {ECD}\)  so le trong do đó: AB // CE.

b) Xét hai tam giác vuông HAD và KED có:

AD = DE (giả thiết)

\(\widehat {HDA} = \widehat {KDE}\)   (hai góc đối đỉnh)

Do đó: \(\Delta HAD = \Delta KED\)  (cạnh huyền - góc nhọn) => AH = EK.

c) Xét hai tam giác MDA và NDE có:

MA = NE (giả thiết)

AD = DE (giả thiết)

\(\widehat {MAD} = \widehat {NED}\)   (hai góc so le trong và AC // BE)

Do đó: \(\Delta MDA = \Delta NDE(c.g.c) \Rightarrow \widehat {MDA} = \widehat {NDE}\)

Mà \(\widehat {MDA} + \widehat {MDE} = {180^0}\)   (hai góc kề bù)

Do đó: \(\widehat {NDE} + \widehat {MDE} = {180^0} \Rightarrow \)   Hai tia DM, DN đối nhau.

Vậy ba điểm M, D, N thẳng hàng.