Bài 8 trang 111 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Cho OM là một bán kính của đường tròn (O). Vẽ đường tròn (O’) có đường kính OM. Một bán
Đề bài
Cho OM là một bán kính của đường tròn (O). Vẽ đường tròn (O’) có đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O’) tại điểm B. Chứng minh cung nhỏ của (O) và cung nhỏ của (O’) có độ dài bằng nhau.
Phương pháp giải - Xem chi tiết
Đặt \(\widehat {AOM} = \alpha \), tính số đo \(\widehat {BO'M}\).
Sử dụng công thức tính độ dài cung n0 của đường tròn có bán kính R là \(l = \dfrac{{\pi Rn}}{{180}}\).
Lời giải chi tiết
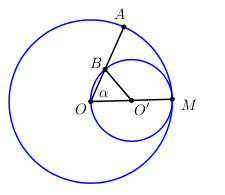
Đặt \(\widehat {AOM} = \alpha \).
Xét tam giác OO’B có: \(O'O = O'B \Rightarrow \Delta OO'B\)cân tại O’ \( \Rightarrow \widehat {O'OB} = \widehat {O'BO} = \alpha \)
\( \Rightarrow \widehat {BO'M} = \widehat {O'OB} + \widehat {O'BO} = 2\alpha \) (góc ngoài bằng tổng 2 góc trong không kề với nó).
Xét đường tròn \(\left( O \right)\) ta có \({l_{MA}} = \dfrac{{\pi OM\alpha }}{{180}}\).
Xét đường tròn \(\left( {O'} \right)\) có \({l_{MB}} = \dfrac{{\pi O'O.2\alpha }}{{180}} = \dfrac{{\pi \left( {2O'O} \right)\alpha }}{{180}} = \dfrac{{\pi OM\alpha }}{{180}}\)
Vậy \({l_{MA}} = {l_{MB}}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 8 trang 111 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







