Bài 7.16 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức
Cho hình chóp S.ABC có SA ( bot ) (ABC). Gọi H là hình chiếu của A trên BC.
Đề bài
Cho hình chóp S.ABC có SA \( \bot \) (ABC). Gọi H là hình chiếu của A trên BC.
a) Chứng minh rằng (SAB) \( \bot \) (ABC) và (SAH) \( \bot \) (SBC).
b) Giả sử tam giác ABC vuông tại A, \(\widehat {ABC} = {30^0},AC = a,SA = \frac{{a\sqrt 3 }}{2}.\) Tính số đo của góc nhị diện [S, BC, A]
Phương pháp giải - Xem chi tiết
- Hai mặt phẳng được gọi là vuông góc nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
- Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải chi tiết
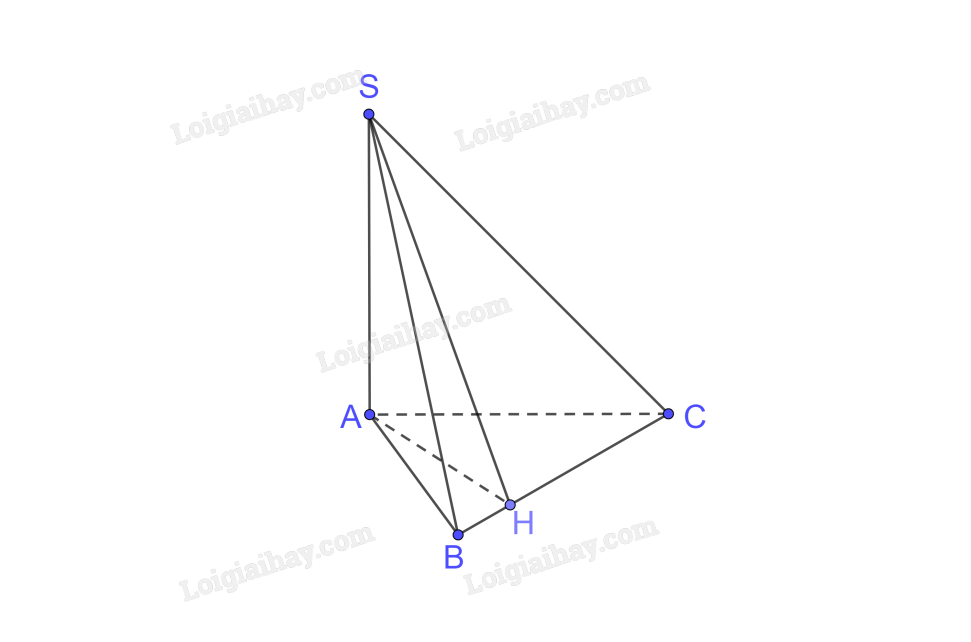
a) \(SA \bot \left( {ABC} \right);SA \subset \left( {SAB} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)\)
\(\left. \begin{array}{l}AH \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AH \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAH} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAH} \right) \bot \left( {SBC} \right)\)
b) Ta có \(AH \bot BC,BC \bot SH\left( {BC \bot \left( {SAH} \right)} \right)\)
\( \Rightarrow \left[ {S,BC,A} \right] = \left( {SH,AH} \right) = \widehat {SHA}\)
Xét tam giác ABC vuông tại A có
\(\widehat {ABC} = {30^0} \Rightarrow \widehat {ACH} = {60^0}\)
Xét tam giác ACH vuông tại H có
\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} \Rightarrow AH = a.\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác SHA vuông tại A có
\(\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1 \Rightarrow \widehat {SHA} = {45^0}\)
Vậy \(\left[ {S,BC,A} \right] = {45^0}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7.16 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức timdapan.com"







