Bài 7 trang 86 SGK Toán 11 tập 1 - Chân trời sáng tạo
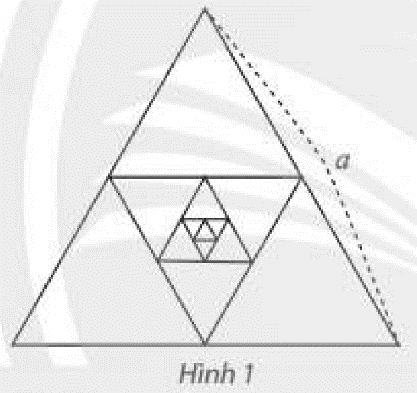
Cho tam giác đều có cạnh bằng \(a\), gọi là tam giác \({H_1}\). Nối các trung điểm của \({H_1}\) để tạo thành tam giác \({H_2}\). Tiếp theo, nối các trung điểm của \({H_1}\), để tạo thành tam giác \({H_3}\) (Hình 1).
Đề bài
Cho tam giác đều có cạnh bằng \(a\), gọi là tam giác \({H_1}\). Nối các trung điểm của \({H_1}\) để tạo thành tam giác \({H_2}\). Tiếp theo, nối các trung điểm của \({H_1}\), để tạo thành tam giác \({H_3}\) (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác \({H_1},{H_2},{H_3},...\)
Tính tổng chu vi và tổng diện tích các tam giác của dãy.
Phương pháp giải - Xem chi tiết
Bước 1: Tìm cạnh của tam giác đều thứ \(n\) dựa vào cạnh của tam giác đều thứ \(n - 1\).
Bước 2: Tính chu vi và diện tích của tam giác đều thứ \(n\).
Bước 3: Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\):
\(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Gọi \({u_n}\) là độ dài cạnh của tam giác đều thứ \(n\).
Ta có: \({u_1} = a;{u_2} = \frac{{{u_1}}}{2};{u_3} = \frac{{{u_2}}}{2};...\)
Từ đó ta thấy \(\left( {{u_n}} \right)\) là một cấp số nhân có số hạng đầu \({u_1} = a\), công bội \(q = \frac{1}{2}\).
Vậy \({u_n} = {u_1}.{q^{n - 1}} = a.{\left( {\frac{1}{2}} \right)^{n - 1}} = \frac{a}{{{2^{n - 1}}}},n = 1,2,3,...\)
Chu vi của tam giác đều thứ \(n\) là: \({p_n} = 3{u_n} = \frac{{3{\rm{a}}}}{{{2^{n - 1}}}},n = 1,2,3,...\)
Tổng chu vi của các tam giác của dãy là:
\({P_n} = 3{\rm{a}} + \frac{{3{\rm{a}}}}{2} + \frac{{3{\rm{a}}}}{{{2^2}}} + ... + \frac{{3{\rm{a}}}}{{{2^{n - 1}}}} + ... = 3{\rm{a}}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\)
Tổng \(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{2}\).
Vậy \(1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2 \Rightarrow {P_n} = 3{\rm{a}}.2 = 6{\rm{a}}\).
Diện tích của hình vuông thứ \(n\) là:
\({s_n} = \frac{{u_n^2\sqrt 3 }}{4} = {\left( {\frac{a}{{{2^{n - 1}}}}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}.{\left( {\frac{1}{{{2^{n - 1}}}}} \right)^2} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n - 1}}}},n = 1,2,3,...\)
Tổng diện tích của các tam giác của dãy là:
\({S_n} = \frac{{{a^2}\sqrt 3 }}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^2}}} + ... + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n - 1}}}} + ... = \frac{{{a^2}\sqrt 3 }}{4}\left( {1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ...} \right)\)
Tổng \(1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ...\) là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\), công bội \(q = \frac{1}{4}\).
Vậy \(1 + \frac{1}{4} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{4^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{4}}} = \frac{4}{3} \Rightarrow {S_n} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{4}{3} = \frac{{{a^2}\sqrt 3 }}{3}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 86 SGK Toán 11 tập 1 - Chân trời sáng tạo timdapan.com"







