Bài 7 trang 6 SBT Hình học 12 Nâng cao

Đề bài

Cho mặt phẳng \(\left( P \right)\) và phép dời hình f có tính chất : f  biến điểm M thành điểm M  khi và chỉ khi M  nằm trên \(\left( P \right)\). Chứng tỏ rằng f là phép đối xứng qua mặt phẳng \(\left( P \right)\).

Lời giải chi tiết

Phép dời hình f biến mọi điểm M nằm trên \(\left( P \right)\) thành chính nó.

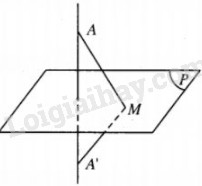
Với điểm A không nằm trên \(\left( P \right)\), ta gọi A^’ là ảnh của A qua f .

Khi đó, nếu \(M \in \left( P \right)\) thì \(MA = M{A'}\).

Vậy \(\left( P \right)\) là mặt phẳng trung trực của AA^’, tức A^’ đối xứng với A qua \(\left( P \right)\).

Vậy f là phép đối xứng qua \(mp\left( P \right)\).