Bài 64 trang 87 SGK Toán 7 tập 2

Đề bài

Gọi \(MH\) là đường cao của tam giác \(MNP.\) Chứng minh rằng: Nếu \(MN < MP\) thì \(HN < HP\)  và  \(\widehat {NMH} < \widehat {PMH}\) (yêu cầu xét hai trường hợp: khi góc \(N\) nhọn và khi góc \(N\) tù).

Lời giải chi tiết

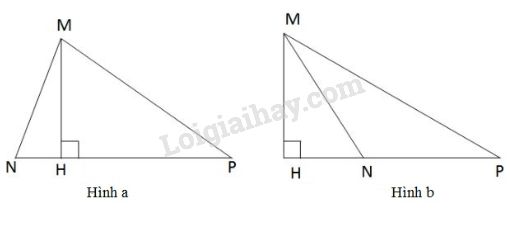
+ Nếu góc \(N\) nhọn (hình a)

\(∆MNP\) có \(\hat N\) nhọn nên chân đường cao \(H\) kẻ từ \(M\) nằm giữa \(N\) và \(P.\)

Ta có hình chiếu của \(MN\) và \(MP\) lần lượt là \(HN\) và \(HP.\)

Từ giả thiết \(MN < MP\) \( \Rightarrow HN < HP\) (quan hệ giữa các đường xiên và hình chiếu).

\(∆MNP\) có \(MN < MP\) \( \Rightarrow\)  \(\widehat {MPN} < \widehat {MNP}\) (quan hệ giữa cạnh và góc trong tam giác)    (1)

Lại có  \(\widehat {NMH} + \widehat {MNH} = {90^o}\) (\(∆MNH\) vuông tại \(H\))   (2)

          \(\widehat {MPH} + \widehat {PMH} = {90^o}\) (\(∆MHP\) vuông tại \(H\))     (3)

Từ (1), (2), (3) suy ra  \(\widehat {NMH} < \widehat {PMH}\)

(Giải thích nếu tổng của hai cặp số cùng bằng nhau (bằng \( 90^o\) chẳng hạn) thì số nào cộng với số lớn hơn thì nhỏ hơn số kia. Tức là:

\(a + b = 90^o ; \quad \quad c + d = 90^o\) 

mà \(b > d\) thì suy ra \(a < c\)) 

+ Nếu góc \(N\) tù (hình b)

\(∆MNP\) có  \(\hat N\) tù nên chân đường cao \(H\) ở ngoài cạnh \(NP\) và \(N\) ở giữa \(H\) và \(P\) (xem lại chứng minh bài 58 trang 83 SGK toán 7 tập 2)

\( \Rightarrow  HN < HP.\)

Vì \(N\) ở giữa \(H\) và \(P\) nên tia \(MN\) ở giữa hai tia \(MH\) và \(MP.\) Từ đó suy ra  \(\widehat {HMN} < \widehat {HMP}\).