Bài 64 trang 57 SGK giải tích 12 nâng cao

Cho hàm số \(y = {{a{x^2} - bx} \over {x - 1}}\)

LG a

Tìm \(a\) và \(b\) biết rằng đồ thị \((C)\) của hàm số đã cho đi qua điểm \(A\left( { - 1;{5 \over 2}} \right)\) và tiếp tuyến của \((C)\) tại điểm \(O(0;0)\) có hệ số bằng \(-3\).

Lời giải chi tiết:

\(y' = {{\left( {2ax - b} \right)\left( {x - 1} \right) - \left( {a{x^2} - bx} \right)} \over {{{\left( {x - 1} \right)}^2}}}\) \(= \frac{{a{x^2} - 2ax + b}}{{{{\left( {x - 1} \right)}^2}}}\)

Đồ thị \((C)\) đi qua \(A\left( { - 1;{5 \over 2}} \right)\) \( \Leftrightarrow y\left( { - 1} \right) = {5 \over 2} \Leftrightarrow {{a + b} \over { - 2}} = {5 \over 2} \) \(\Leftrightarrow a + b =  - 5\,\,\,\left( 1 \right)\)

Tiếp tuyến của \((C)\) tại \(O(0;0)\) có hệ số góc bằng \(-3\) khi và chỉ khi \(y’(0) = -3 \) \( \Leftrightarrow \frac{{a{{.0}^2} - 2a.0 + b}}{{{{\left( {0 - 1} \right)}^2}}} =  - 3\) \( \Leftrightarrow b =  - 3\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(a = -2; b = - 3\).

LG b

Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị của \(a\) và \(b\) đã tìm được.

Lời giải chi tiết:

Với \(a = -2; b = - 3\) ta có: \(y = {{ - 2{x^3} + 3x} \over {x - 1}}\)

Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\)

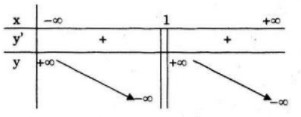
\(y' = {{ - 2{x^2} + 4x - 3} \over {{{(x - 1)}^2}}} < 0\,\forall x \in D\)

Hàm số nghịch biến trên khoảng: \(( - \infty ;1)\) và \((1; + \infty )\)

Hàm số không có cực trị

Giới hạn:

\(\mathop {\lim y}\limits_{x \to  {1^ - }}  =  - \infty ;\,\mathop {\lim y}\limits_{x \to   {1^ + }}  =  + \infty \)

Tiệm cận đứng là: \(x=1\)

\(\eqalign{
& a = \mathop {\lim }\limits_{x \to \infty } {y \over x} \cr&= \mathop {\lim }\limits_{x \to \infty } {{ - 2{x^2} + 3x} \over {{x^2} - x}} = - 2 \cr 
& b = \mathop {\lim }\limits_{x \to \infty } (y + 2x) \cr&= \mathop {\lim }\limits_{x \to \infty } \left( {{{ - 2{x^2} + 3x} \over {x - 1}} + 2x} \right) = 1 \cr} \)

Tiệm cận xiên là: \(y=-2x+1\)

Bảng biến thiên:

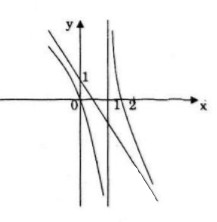
Đồ thị giao \(Oy\) tại điểm \((0;0)\) và \(\left( {{3 \over 2};0} \right)\)