Bài 44 trang 11 SBT Hình học 12 Nâng cao
Giải bài 44 trang 11 sách bài tập Hình học 12 Nâng cao. Khối chóp S.ABCD có đáy là hình bình hành...
Đề bài
Khối chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, AD và SC. Chứng minh mặt phẳng \(\left( {MNP} \right)\) chia khối chóp thành hai phần có thể tích bằng nhau.
Lời giải chi tiết
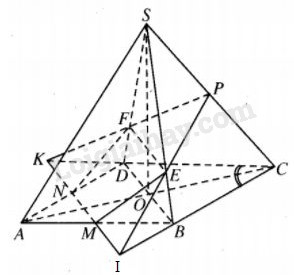
Giả sử đường thẳng MN cắt CD và BC lần lượt tại K và I.
Dễ thấy :
\(\eqalign{ & CK = {3 \over 2}CD,CI = {3 \over 2}CB, \cr & d\left( {P,\left( {ABC} \right)} \right) = {1 \over 2}d\left( {S,\left( {ABC} \right)} \right). \cr & \cr} \)
\({V_{P.CIK}} = {1 \over 3}.{1 \over 2}CI.CK\sin \widehat {ICK} \) .\(d\left( {P,\left( {ABC} \right)} \right)\)
\( = {1 \over 3}.{1 \over 2}.{3 \over 2}CB.{3 \over 2}CD\sin \widehat {BCD} \) .\({1 \over 2}d\left( {S,(ABC)} \right)\)
=\({9 \over {16}}({1 \over 3}CB.CD\sin \widehat {BCD} \) .\(d\left( {S,({\rm{ABC)}}} \right)\)
\( \Rightarrow {V_{P.CIK}} = {9 \over {16}}{V_{S.ABCD}}.\)
Ta có :
\(\eqalign{ & {{{V_{I.BEM}}} \over {{V_{I.CPK}}}} = {{IB} \over {IC}}.{{IE} \over {IP}}.{{IM} \over {IK}}\cr& = {1 \over 3}.{1 \over 2}.{1 \over 3} = {1 \over {18}} \cr & \Rightarrow {V_{I.BEM}} = {1 \over {18}}{V_{I.CPK}} = {1 \over {18}}{V_{P.CIK}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {1 \over {32}}{V_{S.ABCD}}. \cr} \)
Tương tự , ta cũng có \({V_{K.NDF}} = {1 \over {18}}{V_{P.CIK}} = {1 \over {32}}{V_{S.ABCD}}.\)
Vậy nếu gọi V2 là thể tích của phần khối chóp giới hạn bởi \(mp\left( {MNP} \right)\) với mặt phẳng đáy thì :
\(\eqalign{ & {V_2} = {V_{P.CIK}} - \left( {{V_{I.BEM}} + {V_{K.NDF}}} \right) \cr & = {9 \over {16}}{V_{S.ABCD}} - \left( {{1 \over {32}}{V_{S.ABCD}} + {1 \over {32}}{V_{S.ABCD}}} \right) \cr & = {9 \over {16}}{V_{S.ABCD}} - {1 \over {16}}{V_{S.ABCD}} = {1 \over 2}{V_{S.ABCD}}. \cr} \)
Vậy phần còn lại, tức là phần của khối chóp nằm trên \(mp\left( {MNP} \right)\), có thể tích V1 cũng bằng \({1 \over 2}{V_{S.ABCD}}\).
Do đó V1 = V2.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 44 trang 11 SBT Hình học 12 Nâng cao timdapan.com"







