Bài 33 trang 10 SBT Hình học 12 Nâng cao
Giải bài 33 trang 10 sách bài tập Hình học 12 Nâng cao. Cho khối chóp tam giác đều ...
Đề bài
Cho khối chóp tam giác đều \(S.ABC\) có chiều cao bằng h và góc ASB bằng \(2\varphi \). Hãy tính thể tích khối chóp.
Lời giải chi tiết
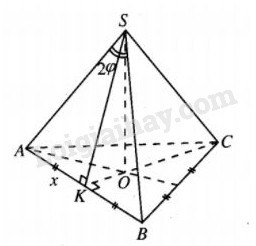
Giả sử O là tâm của tam giác đều ABC.
Khi đó \(SO \bot \left( {ABC} \right)\) và SO = h.
Gọi K là trung điểm của AB. Đặt AK = x.
Khi đó \(\eqalign{ & SK = x\cot \varphi ;\;OK = xtan{30^0} = {x \over {\sqrt 3 }}. \cr & {h^2} = S{K^2} - O{K^2} = {{{x^2}} \over 3}(3{\cot ^2}\varphi - 1) \cr & \Rightarrow {x^2} = {{3{h^2}} \over {3{{\cot }^2}\varphi - 1}}. \cr} \)
Ta có: \(\eqalign{ & {S_{ABC}} = {{A{B^2}\sin {{60}^0}} \over 2} = {x^2}\sqrt 3 , \cr & \Rightarrow {V_{S.ABC}} = {1 \over 3}{S_{ABC}}.h = {{{x^2}\sqrt 3 } \over 3}h \cr&= {{{h^3}\sqrt 3 } \over {3{{\cot }^2}\varphi - 1}}. \cr} \)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 33 trang 10 SBT Hình học 12 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 33 trang 10 SBT Hình học 12 Nâng cao timdapan.com"







