Bài 42 trang 78 Vở bài tập toán 9 tập 2

Cho phương trình \({x^2} - x - 2 = 0\)

LG a

Giải phương trình

Phương pháp giải:

Giải phương trình bằng cách sử dụng

+) Xét phương trình bậc hai: \(a{x^2} + bx + c = 0\,(a \ne 0).\)

 Nếu phương trình có \(a - b + c = 0\) thì phương trình có một nghiệm là \({x_1} =  - 1,\) nghiệm kia là \({x_2} =  - \dfrac{c}{a}.\)

Giải chi tiết:

Xét phương trình \({x^2} - x - 2 = 0\) có \(a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên có hai nghiệm \({x_1} =  - 1;{x_2} = 2.\)

LG b

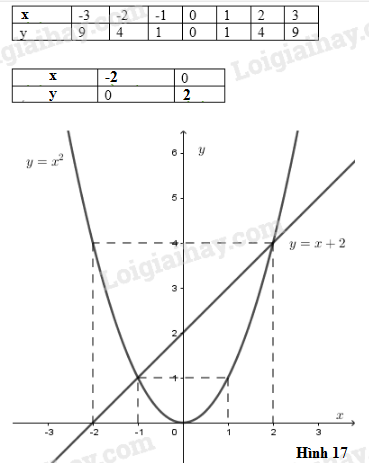
Vẽ hai đồ thị: \(y = {x^2}\) và \(y = x + 2\) trong cùng một hệ trục tọa độ

Phương pháp giải:

Lập bảng giá trị rồi vẽ hai đồ thị hàm số \(y = {x^2};y = x + 2\)

Giải chi tiết:

(h17)

LG c

Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ của các giao điểm của hai đồ thị. 

Phương pháp giải:

Thay hai nghiệm tìm được ở câu a) vào mỗi hàm số để so sánh các giá trị của \(y.\)

Giải chi tiết:

+ Thay \(x =  - 1\) vào đẳng thức \(y = {x^2}\) ta được \(y = {\left( { - 1} \right)^2} = 1\). Điều đó chứng tỏ điểm \(A\left( { - 1;1} \right)\) thuộc đồ thị  của hàm số \(y = {x^2}.\)

Tương tự thay \(x =  - 1\) vào đẳng thức \(y = x + 2\) ta được \(y =  - 1 + 2 = 1\). Điều đó chứng tỏ điểm \(A\left( { - 1;1} \right)\) thuộc đồ thị của hàm số \(y = x + 2.\)

Vậy \(A\left( {1; - 1} \right)\) là giao điểm của hai đồ thị hàm số và nghiệm \(x =  - 1\) là hoành độ của A.

+Tương tự thay \(x = 2\) vào hai đẳng thức \(y = {x^2}\) và \(y = x + 2\) ta đều được \(y = 4\). Điều đó chứng tỏ điểm \(B\left( {2;4} \right)\) thuộc đồ thị của hai hàm số \(y = x + 2\) và \(y = {x^2}.\)

Vậy \(B\left( {2;4} \right)\) là giao điểm của hai đồ thị hàm số và nghiệm \(x = 2\) là hoành độ của B.