Bài 41 trang 127 SGK Đại số 10 nâng cao

Giải và biện luận các hệ bất phương trình

LG a.

\(\left\{ \matrix{
(x - \sqrt 5 )(\sqrt 7 - 2x) > 0 \hfill \cr 
x - m \le 0 \hfill \cr} \right.\)

Phương pháp giải:

Giải từng bất phương trình có trong hệ.

Biện luận m để so sánh các điểm đầu mút, từ đó suy ra tập nghiệm tương ứng.

Lời giải chi tiết:

Ta có bảng xét dấu:

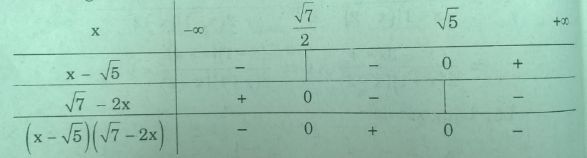
Vậy \((x - \sqrt 5 )(\sqrt 7  - 2x) > 0\) \( \Leftrightarrow {{\sqrt 7 } \over 2} < x < \sqrt 5 \)

Ta có: \({S_1} = ({{\sqrt 7 } \over 2};\sqrt 5 )\)

Bất phương trình thứ hai có nghiệm \(x ≤ m\).

Ta có: \({S_2} = (-∞; m]\),

Do đó:

+ Nếu \(m \le {{\sqrt 7 } \over 2}\) thì tập nghiệm là S = S₁ ∩ S₂ = Ø

+ Nếu \({{\sqrt 7 } \over 2} < m < \sqrt 5 \) thì tập nghiệm là \(S = {S_1} \cap {S_2} = ({{\sqrt 7 } \over 2},m]\)

+ Nếu \(m \ge \sqrt 5 \) thì tập nghiệm là \(S = {S_1} \cap {S_2} = ({{\sqrt 7 } \over 2};\sqrt 5 )\)

LG b.

\(\left\{ \matrix{
{2 \over {x - 1}} < {5 \over {2x - 1}} \hfill \cr 
x - m \ge 0 \hfill \cr} \right.\)

Lời giải chi tiết:

Ta có:

\({2 \over {x - 1}} < {5 \over {2x - 1}} \) \( \Leftrightarrow \frac{2}{{x - 1}} - \frac{5}{{2x - 1}} < 0\) \(\Leftrightarrow {{2(2x - 1) - 5(x - 1)} \over {(x - 1)(2x - 1)}} < 0  \) \( \Leftrightarrow {{-x + 3} \over {(x - 1)(2x - 1)}} < 0\)

Bằng cách lập bảng xét dấu vế trái, ta có:

\({2 \over {x - 1}} < {5 \over {2x - 1}} \Leftrightarrow \left[ \matrix{
{1 \over 2} < x < 1 \hfill \cr 
x > 3 \hfill \cr} \right.\)

Ta có: \({S_1} = ({1 \over 2};1) \cup (3, + \infty )\)

\(x - m \ge 0 \Leftrightarrow x \ge m\) nên tập nghiệm của bất phương trình thứ hai là: S₂ = [m, +∞ ).

Do đó:

+ Nếu \(m \le {1 \over 2}\) thì tập nghiệm là  \({S_1} = ({1 \over 2};1) \cup (3, + \infty )\)

+ Nếu \({1 \over 2} < m < 1\) thì tập nghiệm là \(S = {\rm{[m, 1)}} \cup {\rm{(3, + }}\infty {\rm{)}}\)

+ Nếu \(1≤ m ≤ 3\) thì tập nghiệm là \(S = (3, +∞ )\)

+ Nếu \(m > 3\) thì tập nghiệm là \(S = [m; +∞ )\)