Bài 32 trang 126 SGK Đại số 10 nâng cao

Lập bảng xét dấu của các biểu thức

LG a

\({{4 - 3x} \over {2x + 1}}\)

Phương pháp giải:

- Biến đổi biểu thức về tích, thương các nhị thức bậc nhất.

- Tìm nghiệm của các nhị thức bậc nhất trên.

- Sắp xếp các nghiệm theo thứ tự tăng dần và xét dấu theo chú ý "phải cùng trái khác".

- Từ đó suy ra dấu của biểu thức đã cho.

Lời giải chi tiết:

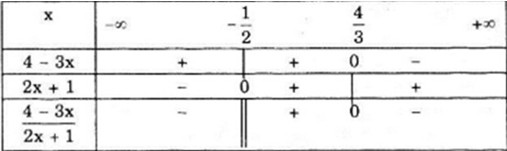
Ta có: \(4 - 3x = 0 \Leftrightarrow x = \dfrac{4}{3};\) \(2x + 1 = 0 \Leftrightarrow x =  - \dfrac{1}{2}\)

Bảng xét dấu:

LG b

\(1 - {{2 - x} \over {3x - 2}}\)

Lời giải chi tiết:

Ta có: \(1 - \frac{{2 - x}}{{3x - 2}} = \frac{{3x - 2 - 2 + x}}{{3x - 2}} = \frac{{4x - 4}}{{3x - 2}}\)

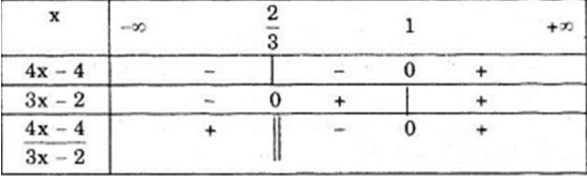
\(4x - 4 = 0 \Leftrightarrow x = 1;\) \(3x - 2 = 0 \Leftrightarrow x = \frac{2}{3}\)

Ta có bảng xét dấu:

LG c

\(x{(x - 2)^2}(3 - x)\)

Lời giải chi tiết:

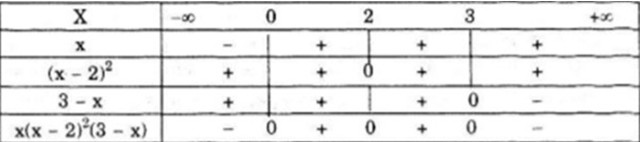
\(x - 2 = 0 \Leftrightarrow x = 2;\) \(3 - x = 0 \Leftrightarrow x = 3\)

Ta có bảng xét dấu sau:

LG d

\({{x{{(x - 3)}^2}} \over {(x - 5)(1 - x)}}\)

Lời giải chi tiết:

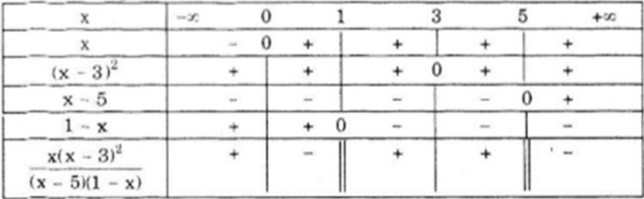
\(x - 3 = 0 \Leftrightarrow x = 3;\) \(x - 5 = 0 \Leftrightarrow x = 5;\) \( 1 - x = 0 \Leftrightarrow x = 1\)

Ta có bảng xét dấu sau: