Bài 39 trang 73 SGK Toán 7 tập 2
Giải bài 39 trang 73 SGK Toán 7 tập 2. Cho hình bên.
Đề bài
Cho hình \(39.\)
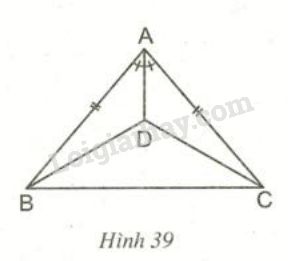
a) Chứng minh \(∆ABD = ∆ACD.\)
b) So sánh góc \(DBC\) với góc \(DCB.\)
Phương pháp giải - Xem chi tiết
- Chứng minh \(∆ABD = ∆ACD\) theo trường hợp bằng nhau thứ hai của tam giác.
- Chứng minh tam giác \(BDC\) là tam giác cân, từ đó suy ra \(\widehat{DBC}= \widehat{DCB}\).
Lời giải chi tiết
a) Xét \(∆ABD\) và \(∆ACD\) ta có:
+) \(AB = AC\) (giả thiết)
+) \(\widehat{BAD}= \widehat{CAD}\) (giả thiết)
+) \(AD\) cạnh chung
Vậy \(∆ABD = ∆ACD\) (c.g.c)
b) Vì \(∆ABD = ∆ACD\) (chứng minh trên)
\( \Rightarrow BD = CD \) ( \(2\) cạnh tương ứng)
\( \Rightarrow ∆BCD\) cân tại \(D\)
\( \Rightarrow \) \(\widehat{DBC}= \widehat{DCB}\) ( tính chất tam giác cân) (điều phải chứng minh).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 39 trang 73 SGK Toán 7 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 39 trang 73 SGK Toán 7 tập 2 timdapan.com"







