Bài 3 trang 115 SGK Toán 8 tập 1

Đề bài

Cho hình thoi \(ABCD\) có \(\widehat A = {60^0}\). Gọi \(E, F, G, H\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DA\). Chứng minh rằng đa giác \(EBFGDH\) là lục giác đều.

Lời giải chi tiết

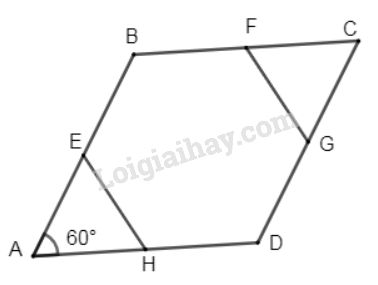
\(ABCD\) là hình thoi (giả thiết) và \(\widehat A = {60^0}\) (giả thiết)

Do đó \(AB = BC = CD = DA\); \(AB//DC;\,BC//AD\).

\(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\) nên \(AE = EB = BF = FC = CG = GD\)\(\, = DH = HA\)

\(\widehat A + \widehat {ABC} = {180^0}\) (\(2\) góc trong cùng phía bù nhau)

\( \Rightarrow \widehat {ABC} = {180^0} - \widehat A = {180^0} - {60^0} \)\(= {120^0}\)

\( \Rightarrow \widehat {ABC} = \widehat {ADC} = {120^0}\) (tính chất hình thoi)

\(\Delta EAH\) là tam giác đều (vì tam giác cân có một góc \(60^0\))

\( \Rightarrow \widehat {AEH} = \widehat {AHE} = {60^0}\) (tính chất tam giác đều)

\(\left\{ \begin{array}{l}
\widehat {AEH} + \widehat {HEB} = {180^0}\\
\widehat {AHE} + \widehat {EHD} = {180^0}
\end{array} \right.\)  (hai góc kề bù)

\( \Rightarrow \widehat {HEB} = \widehat {EH{\rm{D}}} = {180^0} - {60^0} = {120^0}\)

 Tương tự: \(\widehat {BFG} = {120^0},\widehat{F GD} = {120^0}\)

Vậy đa giác \(EBFGDH\) có tất cả các góc bằng nhau, mặt khác \(EBFGDH\) cũng có tất cả các cạnh bằng nhau ( bằng nửa cạnh hình thoi)

Vậy \(EBFGDH\) là một lục giác đều (dấu hiệu nhận biết lục giác đều)