Bài 24 trang 199 SGK Đại số và Giải tích 12 Nâng cao

Giải các phương trình sau trên C và biểu diễn hình hợp tập hợp các nghiệm của mỗi phương trình (trong mặt phẳng phức):

LG a

\({z^3} + 1 = 0\);

Phương pháp giải:

Phân tích vế trái thành nhân tử, đưa về giải phương trình tích.

\(AB = 0 \Leftrightarrow \left[ \begin{array}{l}
A = 0\\
B = 0
\end{array} \right.\)

Lời giải chi tiết:

\({z^3} + 1 = 0 \Leftrightarrow \left( {z + 1} \right)\left( {{z^2} - z + 1} \right) = 0\)

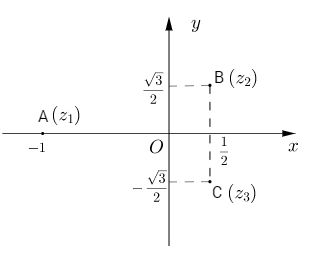
Nghiệm của \(z + 1 = 0\) là \({z_1} =  - 1\)

\({z^2} - z + 1 = 0 \) \(\Leftrightarrow {\left( {z - {1 \over 2}} \right)^2} =  - {3 \over 4} = {\left( {{{\sqrt 3 } \over 2}i} \right)^2}\)              

\( \Leftrightarrow \left[ \matrix{  z = {1 \over 2} + {{\sqrt 3 } \over 2}i = {z_2} \hfill \cr  z = {1 \over 2} - {{\sqrt 3 } \over 2}i = {z_3} \hfill \cr}  \right.\)

Vậy \(S = \left\{ { - 1;{1 \over 2} + {{\sqrt 3 } \over 2}i;{1 \over 2} - {{\sqrt 3 } \over 2}i} \right\}\)

LG b

\({z^4} - 1 = 0\);

Phương pháp giải:

Phân tích vế trái thành nhân tử, đưa về giải phương trình tích.

Lời giải chi tiết:

\({z^4} - 1 = 0 \Leftrightarrow \left( {{z^2} - 1} \right)\left( {{z^2} + 1} \right) = 0\)

\( \Leftrightarrow \left[ \matrix{  {z^2} - 1 = 0 \hfill \cr  {z^2} + 1 = 0 \hfill \cr}  \right. \Leftrightarrow \left[ \matrix{  z =  \pm 1 \hfill \cr  z =  \pm i \hfill \cr}  \right.\)

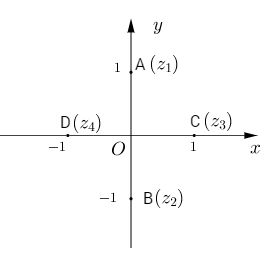
Phương trình có 4 nghiệm \({z_1} = i,{z_2} =  - i,{z_3} = 1,{z_4} =  - 1\)

LG c

\({z^4} + 4 = 0\)

Phương pháp giải:

Phân tích vế trái thành nhân tử, đưa về giải phương trình tích.

Lời giải chi tiết:

\({z^4} + 4 = 0\) \( \Leftrightarrow {z^4} - {\left( {2i} \right)^2} = 0 \) \(\Leftrightarrow \left( {{z^2} + 2i} \right)\left( {{z^2} - 2i} \right) = 0\)

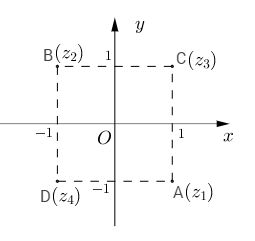
Nghiệm của \({z^2} + 2i = 0\) là các căn bậc hai của -2i, đó là \({z_1} = 1 - i\),\({z_2} =  - 1 + i\)

(Do \({\left( {1 - i} \right)^2} = 1 - 2i - 1 =  - 2i\))

Nghiệm của \({z^2} - 2i = 0\) là các căn bậc hai của 2i, đó là \({z_3} = 1 + i\),\({z_4} =  - 1 - i\)

(Do \({\left( {1 + i} \right)^2} = 1 + 2i - 1 =   2i\))

Vậy \({z^4} + 4 = 0\) có bốn nghiệm \({z_1},{z_2},{z_3},{z_4}\).

LG d

\(8{z^4} + 8{z^3} = z + 1\).

Phương pháp giải:

Phân tích vế trái thành nhân tử, đưa về giải phương trình tích.

Lời giải chi tiết:

\(8{z^4} + 8{z^3} = z + 1 \Leftrightarrow \left( {z + 1} \right)\left( {8{z^3} - 1} \right) = 0\)

\( \Leftrightarrow \left( {z + 1} \right)\left( {2z - 1} \right)\left( {4{z^2} + 2z + 1} \right) = 0\)

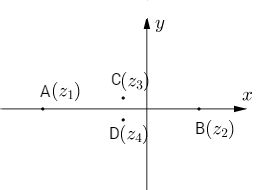
Nghiệm của \(z + 1 = 0\) là \({z_1} =  - 1\)

Nghiệm của \(2z - 1 = 0\) là \({z_2} = {1 \over 2}\)

Phương trình \(4{z^2} + 2z + 1 = 0\) có \(\Delta ' = 1 - 4 =  - 3\) nên có nghiệm là \({z_3} =  - {1 \over 4} + {{\sqrt 3 } \over 4}i\) và \({z_4} =  - {1 \over 4} - {{\sqrt 3 } \over 4}i\)

Vậy phương trình đã cho có bốn nghiệm\({z_1},{z_2},{z_3},{z_4}\)