Bài 2 trang 134 SGK Toán 9 tập 2
Giải bài 2 trang 134 SGK Toán 9 tập 2. Tam giác ABC có góc B = 45o, góc C = 30o. Nếu AC = 8 thì AB bằng:
Đề bài
Tam giác \(ABC\) có góc \(\widehat B = {45^0},\) góc \(\widehat C = {30^0}.\) Nếu \(AC = 8\) thì \(AB\) bằng:
(A) \(4\) (B) \(4\sqrt2\)
(C) \(4\sqrt3\) (D) \(4\sqrt6\)
Hãy chọn câu trả lời đúng.
Phương pháp giải - Xem chi tiết
+) Áp dụng công thức tỉ số lượng giác của góc nhọn và các hệ thức lượng trong tam giác vuông.
Lời giải chi tiết
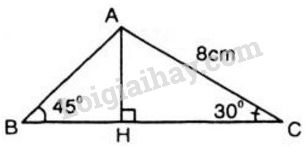
Hạ \(AH \bot BC\) \((H \in BC).\)
Trong tam giác vuông \(HAC\) \((\widehat H = {90^0})\) có \(\widehat{C}=30^0.\)
\(\Rightarrow AH = AC.\sin 30^0=8.\dfrac {1}2 = 4(cm).\)
Xét \(∆HAB\) là tam giác vuông cân tại \(H\) có:
\(AH = BH = 4\) \((cm).\)
Áp dụng định lí Py-ta-go trong tam giác vuông \(HAB\) ta có:
\(AB = \sqrt {H{A^2} + H{B^2}} = \sqrt {{4^2} + {4^2}} = \sqrt {32} = 4\sqrt 2\)
Vậy \(AB = 4\sqrt2\) \(cm.\)
Chọn đáp án B.
Search google: "từ khóa + timdapan.com" Ví dụ: " Bài 2 trang 134 SGK Toán 9 tập 2 timdapan.com"