Đề thi học sinh giỏi môn Toán lớp 8

Đề thi học sinh giỏi môn Toán lớp 8 phòng GD&ĐT Nam Trực, Nam Định năm 2015 - 2016 có đáp án kèm theo được TimDapAnsưu tầm và giới thiệu là tài liệu bồi dưỡng học sinh giỏi môn Toán giúp các bạn học sinh tự ôn tập kiến thức, làm quen với dạng đề thi học sinh giỏi. Mời các bạn tham khảo.

Đề thi học sinh giỏi môn Lịch sử lớp 8 phòng GD&ĐT Nam Trực, Nam Định năm 2015 - 2016

Đề thi học sinh giỏi môn Ngữ văn lớp 8 phòng GD&ĐT Nam Trực, Nam Định năm 2015 - 2016

Bài 1: (4,0 điểm)

Cho biểu thức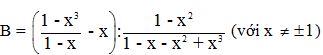

1) Rút gọn biểu thức B.

2) Tìm giá trị của x để B < 0.

3) Tính giá trị của biểu thức B với x thỏa mãn: Ix - 4I = 5

Bài 2: (4,0 điểm)

1) Giải phương trình: x⁴ + 3x³ + 4x² + 3x + 1 = 0

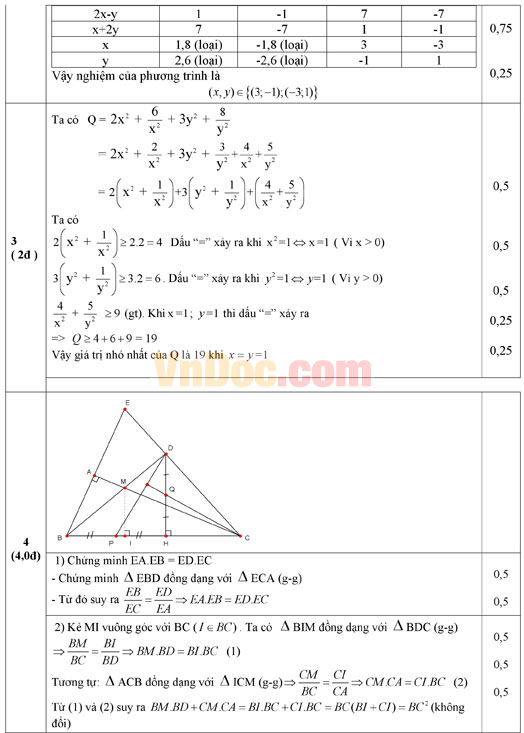
2) Giải phương trình nghiệm nguyên: 2x² + 3xy – 2y² = 7

Bài 3: (2,0 điểm) Cho hai số thực dương x, y thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức: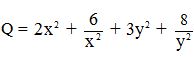

Bài 4: (4,0 điểm) Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E.

1) Chứng minh: EA.EB = ED.EC.

2) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD+CM.CA có giá trị không đổi.

3) Kẻ DH ⊥ BC (H ∈ BC). Gọi P, Q lần lượt là trung điểm của các đoạn thẳng BH, DH. Chứng minh CQ ⊥ PD.

Bài 5: (4,0 điểm) Cho tam giác ABC nhọn, các đường cao AA', BB', CC' và H là trực tâm

1) Tính tổng

2) Gọi AI là phân giác của tam giác ABC; IM và IN theo thứ tự là phân giác của ∠AIC và ∠AIB. Chứng minh: AN.BI.CM = BN.IC.AM

Bài 6: (2,0 điểm) Cần dùng ít nhất bao nhiêu tấm bìa hình tròn có bán kính bằng 1 để phủ kín một tam giác đều có cạnh bằng 3, với giả thiết không được cắt tấm bìa.

Đáp án đề thi học sinh giỏi môn Toán lớp 8