Đề thi học kì 2 môn Toán lớp 7

Đề thi học kì 2 môn Toán lớp 7 trường THCS Bùi Hữu Diên, Thái Bình năm học 2016 - 2017 gồm 2 phần trắc nghiệm và tự luận, có đáp án đi kèm. Đây là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 7, giúp các bạn luyện tập và củng cố kiến thức môn Toán hiệu quả. Chúc các bạn học tốt.

Bộ đề thi học kì 2 môn Toán lớp 7 TP. Hồ Chí Minh năm 2014 - 2015

Đề cương ôn tập học kì 2 môn Toán lớp 7

Đề thi học kì 2 môn Toán lớp 7 phòng GD&ĐT Đại Thành, Bắc Giang năm 2015 - 2016

Phần I. Trắc nghiệm khách quan: (2 điểm)

Câu 1) Đơn thức đồng dạng với đơn thức 5 là:

A. 3xy B. -1/3.3x²y C. 3xy² + 1 D. xy²

Câu 2) Giá trị của biểu thức tại x = -2 và y = -1 là:

A. - 4 B. 12 C. -10 D. -12

Câu 3) Cho tam giác ABC có Â = 90⁰ và AB = AC ta có:

A. là tam giác vuông. B. là tam giác cân.

C. là tam giác vuông cân. D. là tam giác đều.

Câu 4) Một tam giác có G là trọng tâm, thì G là giao điểm của ba đường:

A. Ba đường cao B. Trung trực C. Phân giác D. Trung tuyến

Câu 5) Biểu thức nào sau đây không là đơn thức:

A. 4x²y B. 7 + xy² C. 6xy.(-x³) D. -4xy²

Câu 6) Bậc của đơn thức 5x³y2x²z là:

A. 3 B. 5 C. 7 D. 8

Câu 7) Cho tam giác ABC có: AB = 3 cm; BC = 4cm; AC = 5cm. Thì:

A. góc A lớn hơn góc B B. góc B nhỏ hơn góc C

C. góc A nhỏ hơn góc C D. góc B lớn hơn góc C

Câu 8) Cho tam giác ABC cân tại A, góc A = 30⁰. Trên nửa mặt phẳng bờ AB có chứa C, vẽ tia Bx vuông BA. Trên tia Bx lấy điểm N sao cho BN = BA. Số đo góc BCN là:

A. 90⁰ B. 120⁰ C. 150⁰ D. 180⁰

Phần II. Tự luận: (8 điểm)

Bài 1. (2 điểm) Cho đơn thức

a) Thu gọn đơn thức b) Chỉ rõ phần hệ số, phần biến của đơn thức

c) Tìm bậc của đơn thức d) Tính giá trị của đơn thức tại x = -1, y = 2

Bài 2. (2,5 điểm) Cho 2 đa thức: A = 2x³ + x² – 4x + x³ + 3; B = 6x + 3x³ - 2x + x² – 5

a) Tính tổng hai đa thức: A + B

b) Tính hiệu hai đa thức: A - B

c) Tìm nghiệm của đa thức hiệu A – B vừa tìm được ở ý b.

Bài 3. (3 điểm) Cho tam giác ABC vuông tại A, có AB = 9cm, BC = 15cm.

a) Tính độ dài cạnh AC và so sánh các góc của tam giác ABC.

b) Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD.

Chứng minh tam giác BCD cân.

c) E là trung điểm cạnh CD, BE cắt AC ở I. Chứng minh DI đi qua trung điểm cạnh BC

Bài 4. (0,5 điểm) Tính tỉ số biết và

------- Hết -------

Đáp án đề thi học kì 2 môn Toán lớp 7

Phần I- Trắc nghiệm khách quan: (2 điểm)

Phần II- Tự luận: (8 điểm)

Câu 1 (2đ)

a)

b) Phần hệ số: 1/3, phần biến: x³y²

c) Bậc của đơn thức: 5

d) Tại x = -1, y = 2 ta có M = -4/3

Câu 2 (2,5đ)

a) A + B = 6x³ + 2x² – 2

b) A - B = - 8x + 8

c) Cho -8x + 8 = 0

-8x = -8

x = 1

Câu 3 (3đ)

a) Dùng định lý Py-ta-go tính AC = 12cm, vì AB < AC < BC nên góc C < góc B < góc A

b) ΔABC = ΔADC nên BC = DC hay ΔBCD cân tại C

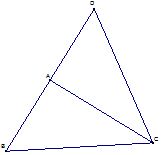
c, Kẻ hình, chứng minh được I là trọng tâm tam giác BCD.

Vì I là trọng tâm suy ra DI là đường trung tuyến tam giác BCD.

Nên suy ra DI là đường trung tuyến tam giác BCD, do đó DI đi qua trung điểm cạnh BC.

Câu 4 (0,5đ) Tìm được đúng