Lý thuyết Định lí thalès trong tam giác SGK Toán 8 - Chân trời sáng tạo
Định lí Thales là gì?
1. Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là: \(\frac{{AB}}{{CD}}\)
Chú ý:
- Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.
- Tỉ số của hai đoạn thẳng đó không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.
Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A'B}}{{C'D}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\)
2. Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
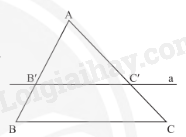
\(\begin{array}{l}\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\\ \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}};\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\end{array}\)
3. Hệ quả của định lí Thalès
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
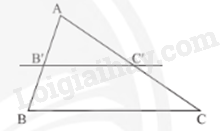
\(\begin{array}{l}\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\\ \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\end{array}\)
4. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
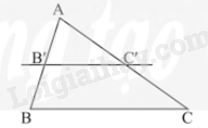
\(\Delta ABC,B' \in AB,C' \in AC,\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} \Rightarrow B'C'//BC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Định lí thalès trong tam giác SGK Toán 8 - Chân trời sáng tạo timdapan.com"







