Luyện tập 6 trang 106 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho hình thang ABCD (AB // CD, AB < CD). Gọi E là trung điểm của BD, F là trung điểm của AC. Chứng minh rằng
Đề bài
Cho hình thang ABCD (AB // CD, AB < CD). Gọi E là trung điểm của BD, F là trung điểm của AC. Chứng minh rằng \(EF = {{CD - AB} \over 2}\)
Lời giải chi tiết
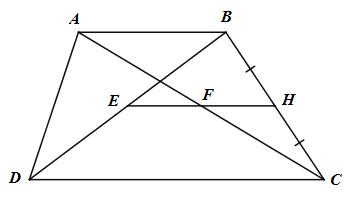
Gọi H là trung điểm của BC
Ta có: F, H lần lượt là trung điểm của AC và BC
=> FH là đường trung bình của tam giác ABC.
=> FH // AB và \(FH = {1 \over 2}AB\)
E; H lần lượt là trung điểm của DB và BC
=> EH là đường trung bình của tam giác BDC
=> EH // CD và \(EH = {1 \over 2}CD\)
Ta có FH // AB, AB // CD => FH // CD
FH // CD, EH // CD
=> FH, EH trùng nhau (tiên đề Ơ-clit) => E, F, H thẳng hàng.
Do đó \(EF = EH - FH = {{CD} \over 2} - {{AB} \over 2} = {{CD - AB} \over 2}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Luyện tập 6 trang 106 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Luyện tập 6 trang 106 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"