Luyện tập 5 trang 106 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của AC và BC.
Đề bài
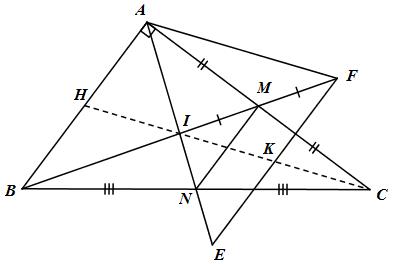
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của AC và BC.
a) Chứng minh rằng tứ giác AMNB là hình thang vuông.
b) Gọi I là giao điểm của BM và AN. Trên tia đối của tia NA lấy điểm E sao cho NE = NI. Trên tia đối của tia MB lấy điểm F sao cho NE = NI. Trên tia đối của tia MB lấy điểm F sao cho MF = MI. Chứng minh rằng EF // AB.
c) Gọi H là trung điểm của AB, K là trung điểm của EF. Chứng minh rằng bốn điểm C, K, I, H thẳng hàng.
Lời giải chi tiết
a) ∆ABC có:
M là trung điểm của AC (gt);
N là trung điểm của BC (gt);
=> MN là đường trung bình của tam giác ABC.
=> MN // AB=> Tứ giác AMNB là hình thang.
Mà \(\widehat {MAB} = 90^\circ \)
Nên tứ giác AMNB là hình thang vuông.
b) ∆IEF có :
M là trung điểm của IF (gt) ;
N là trung điểm của IE (gt);
=> MN là đường trung bình của tam giác IEF => MN // EF
Mà MN // AB (chứng minh câu a) nên \(EF // AB\)
c) ∆ABC có hai đường trung tuyến BM và AN cắt nhau tại I
=> I là trọng tâm của tam giác ABC.
Mà CH là đường trung tuyến của tam giác ABC (H là trung điểm của AB)
Nên CH đi qua I => C, H, I thẳng (1).
∆ABC có I là trọng tâm và BM là đường trung tuyến \( \Rightarrow \left\{ \matrix{ BI = {2 \over 3}BM \hfill \cr IM = {1 \over 3}BM \hfill \cr} \right.\)
\( \Rightarrow {{BI} \over {IM}} = 2 \Rightarrow BI = 2IM\)
Mà 2IM = IF (do M là trung điểm của IF) nên BI = IF => I là trung điểm của BF.
∆ABF có:
I là trung điểm của BF;
H là trung điểm của AB
=> IH là đường trung bình của tam giác ABF => IH // AF
Ta có:
AI = 2IN (I là trọng tâm của tam giác ABC và AN là đường trung tuyến)
2IN = IE (N là trung điểm của IE)
=> AI = IE => I là trung điểm của AE.
Mà K là trung điểm của EF.
Nên IK là đường trung bình của tam giác AEF => IK // AF
Lại có : IH // AF.
Do đó H, I, K thẳng hàng (2)
Từ (1) và (2) suy ra C, K, I, H thẳng hàng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Luyện tập 5 trang 106 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"