Hoạt động 18 trang 122 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập a) Cho tam giác ABC vuông tài A, O là trung điểm BC. Lấy trung điểm BC. Lấy điểm D đối xứng với điểm A qua O (h.35a). Chứng minh rằng tứ giác ABCD là hình chữ nhật.
Đề bài
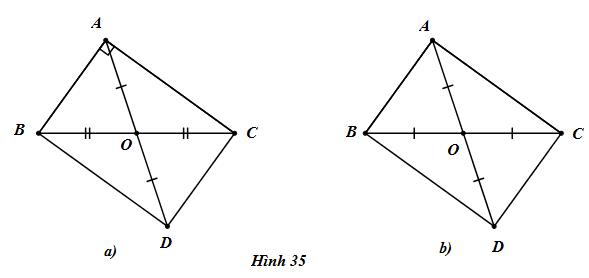
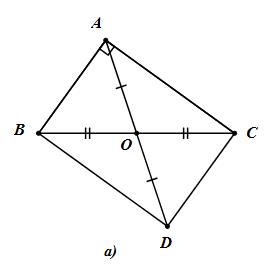
a) Cho tam giác ABC vuông tài A, O là trung điểm BC. Lấy trung điểm BC. Lấy điểm D đối xứng với điểm A qua O (h.35a). Chứng minh rằng tứ giác ABCD là hình chữ nhật.
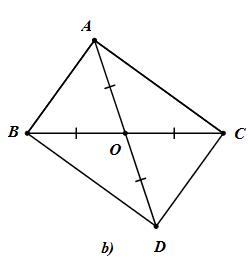
b) Cho tam giác ABC có điểm O thuộc BC sao cho \(OA = OB = OC = {1 \over 2}BC\) . Lấy điểm D đối xứng với điểm A qua O (h.35b). Chứng minh rằng tứ giác ABCD là hình chữ nhật.
Lời giải chi tiết
a) Tứ giác ABCD có:
O là trung điểm của BC (gt)
O là trung điểm của AD (gt)
Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mà \(\widehat {BAC} = {90^0}\) (gt)
Nên tứ giác ABCD là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
b) Tứ giác ABCD có:
O là trung điểm của BC (OB = OC)
O là trung điểm của AD (OA = OD)
Do đó tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mặt khác \(OA = {1 \over 2}AD\) (O là trung điểm của AD);
\(OB = {1 \over 2}BC\)
Và OA = OB (gt) => AD = BC
Hình bình hành ABCD có AD = BC , do đó tứ giác ABCD là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật).
Search google: "từ khóa + timdapan.com" Ví dụ: "Hoạt động 18 trang 122 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"