Bài 174 : Luyện tập chung

Bài 1

Viết vào ô trống (theo mẫu) :

Phương pháp giải:

Khi viết số ta viết các chữ số từ trái sang phải, hay viết từ hàng cao tới hàng thấp.

Lời giải chi tiết:

Bài 2

Viết số thích hợp vào chỗ chấm :

Phương pháp giải:

 Dựa vào bảng đơn vị đo khối lượng:

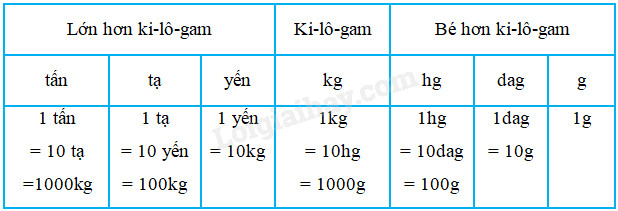
Lời giải chi tiết:

Bài 3

Tính : 

a) \(\dfrac{3}{4} + \dfrac{1}{2} + \dfrac{5}{8} \)

b) \(\dfrac{5}{7} + \dfrac{9}{8} - \dfrac{{15}}{{28}} \)

c) \(\dfrac{{11}}{{30}} - \dfrac{9}{{25}} \times \dfrac{{15}}{{27}} \)

d) \(\dfrac{3}{4}:\dfrac{5}{8}:\dfrac{3}{{10}} \)

Phương pháp giải:

Biểu thức có các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau.

Lời giải chi tiết:

a) \(\dfrac{3}{4} + \dfrac{1}{2} + \dfrac{5}{8} = \dfrac{{6 }}{8} + \dfrac{4}{8}+ \dfrac{5}{8} \)\(= \dfrac{{10}}{8} + \dfrac{5}{8} = \dfrac{{15}}{8}\)

b) \(\dfrac{5}{7} + \dfrac{9}{8} - \dfrac{{15}}{{28}} = \dfrac{{40 }}{{56}}+ \dfrac{63}{56} - \dfrac{{15}}{{28}}\)\(= \dfrac{{103}}{{56}} - \dfrac{{15}}{{28}} = \dfrac{{103 }}{{56}}- \dfrac{30}{56} = \dfrac{{73}}{{56}}\)

c) \( \dfrac{{11}}{{30}} - \dfrac{9}{{25}} \times \dfrac{{15}}{{27}} = \dfrac{{11}}{{30}} - \dfrac{{9 \times 15}}{{25 \times 27}}\)\(=  \dfrac{{11}}{{30}} - \dfrac{{9 \times 5 \times 3}}{{5 \times 5 \times  9\times 3}}= \dfrac{{11}}{{30}} - \dfrac{1}{5}\)\(= \dfrac{{11 }}{{30}}-  \dfrac{6}{30}= \dfrac{5}{{30}} = \dfrac{1}{6}\)

d) \(\dfrac{3}{4}:\dfrac{5}{8}:\dfrac{3}{{10}} = \dfrac{3}{4} \times \dfrac{8}{5} \times \dfrac{{10}}{3} \)\( =\dfrac{3 \times 8 \times 10}{4 \times 5 \times 3}= \dfrac{3 \times 4 \times 2 \times 5 \times 2}{4 \times 5 \times 3}\)\(= 4\)

Bài 4

Có 40 học sinh đang tập hát, trong đó số học sinh trai bằng\(\dfrac{3}{5}\) số học sinh gái. Hỏi có bao nhiêu học sinh trai đang tập hát?

Phương pháp giải:

1. Vẽ sơ đồ: coi số học sinh trai gồm 3 phần bằng nhau thì số học sinh gái gồm 5 phần như thế.

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số học sinh trai đang tập hát (lấy giá trị một phần nhân với số phần biểu diễn số học sinh trai).

Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước.

Lời giải chi tiết:

Ta có sơ đồ : 

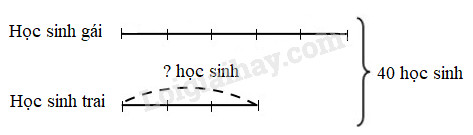
Theo sơ đồ, tổng số phần bằng nhau là :

3 + 5 = 8 (phần)

Số học sinh trai đang tập hát là :

40 : 8 × 3 = 15 (học sinh)

                          Đáp số: 15 học sinh.

Bài 5

Hình nào có đặc điểm thích hợp thì tích dấu (x) vào ô trống tương ứng:

Phương pháp giải:

- Dựa vào tính chất của các hình.

- Có thể vẽ hình ra nháp để quan sát lại.

Lời giải chi tiết: