Bài 159 : Ôn tập về phân số
Giải bài tập 1, 2, 3, 4 trang 92, 93 VBT toán 4 bài 159 : Ôn tập về phân số với lời giải chi tiết và cách giải nhanh, ngắn nhất
Bài 1
Nối phân số \(\displaystyle{2 \over 5}\) với hình biểu thị phân số đó :
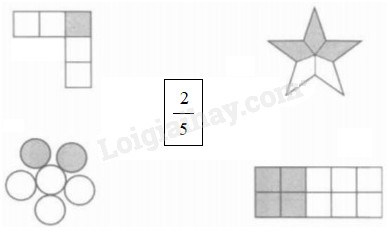
Phương pháp giải:
Quan sát hình vẽ và tìm phân số chỉ số phần tô màu của từng hình.
Lời giải chi tiết:
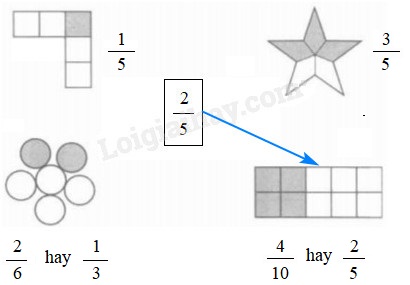
Bài 2
Viết tiếp vào chỗ chấm :
Phương pháp giải:
Quan sát hình vẽ và điền phân số thích hợp vào chỗ chấm.
Lời giải chi tiết:
Bài 3
Rút gọn phân số:
\(\displaystyle {{15} \over {18}}\) ; \(\displaystyle {{14} \over {40}}\) ; \(\displaystyle {{18} \over {24}}\)
\(\displaystyle {{25} \over {35}}\) ; \(\displaystyle {{60} \over {12}}\) ; \(\displaystyle {{100} \over {1000}}\)
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn .
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
Rút gọn phân số:
\(\displaystyle {{15} \over {18}}= \dfrac{15:3}{18:3} = \dfrac{5}{6}\) ; \(\displaystyle {{14} \over {40}}=\dfrac{14:2}{40:2} = \dfrac{7}{20}\) ; \(\displaystyle {{18} \over {24}}=\dfrac{18:6}{24:6} = \dfrac{3}{4}\)
\(\displaystyle {{25} \over {35}}=\dfrac{25:5}{35:5} = \dfrac{5}{7}\) ; \(\displaystyle {{60} \over {12}}=\dfrac{60:12}{12:12} = \dfrac{5}{1}=5\) ; \(\displaystyle {{100} \over {1000}}=\dfrac{100:100}{1000:100} = \dfrac{1}{10}\)
Bài 4
Quy đồng mẫu số các phân số:
a) \(\displaystyle {3 \over 5}\) và \(\displaystyle {4 \over 7}\) b)\(\displaystyle {1 \over 4};{1 \over 5}\) và\(\displaystyle {1 \over 2}\)
Phương pháp giải:
Khi quy đồng mẫu số hai phân số có thể làm như sau:
- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.
- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.
Lời giải chi tiết:
a) \(\displaystyle {3 \over 5}\) và \(\displaystyle {4 \over 7}\)
\(\displaystyle \eqalign{ & {3 \over 5} = {{3 \times 7} \over {5 \times 7}} = {{21} \over {35}} \cr& {4 \over 7} = {{4 \times 5} \over {7 \times 5}} = {{20} \over {35}} \cr} \)
b) \(\displaystyle {1 \over 4};{1 \over 5}\) và\(\displaystyle {1 \over 2}\)
\(\displaystyle \eqalign{& {1 \over 4} = {{1 \times 5} \over {4 \times 5}} = {5 \over {20}} \cr & {1 \over 5} = {{1 \times 4} \over {5 \times 4}} = {4 \over {20}} \cr & {1 \over 2} = {{1 \times 10} \over {2 \times 10}} = {{10} \over {20}} \cr} \)
Bài 5
Sắp xếp các phân số \(\displaystyle {1 \over 3};{1 \over 6};{2 \over 5};{3 \over 2}\) theo thứ tự từ bé đến lớn.
Phương pháp giải:
So sánh các phân số đã cho rồi sắp xếp các phân số theo thứ tự từ bé đến lớn.
Lời giải chi tiết:
Nhận xét:
\(\dfrac{1}{3} < 1\) ; \(\dfrac{1}{6} < 1\) và \(\dfrac{1}{6}< \dfrac{1}{3}\) ;
\(\dfrac{5}{2} > 1\) ; \(\dfrac{3}{2} > 1\) và \(\dfrac{3}{2} < \dfrac{5}{2}\).
Do đó : \(\dfrac{1}{6} < \dfrac{1}{3}<\dfrac{3}{2} < \dfrac{5}{2}\).
Vậy các phân số đã cho xếp theo thứ tự tăng dần là :
\(\displaystyle{1 \over 6}\;;\;\;{1 \over 3}\;;\;\;{3 \over 2}\;;\;\;{5 \over 2}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 159 : Ôn tập về phân số timdapan.com"









