Phần câu hỏi bài 6 trang 131 Vở bài tập toán 7 tập 1

Câu 12.

Một tam giác cân có góc ở đỉnh bằng \({50^o}.\)  Góc ở đáy tam giác cân đó bằng:

\(\begin{array}{l}(A)\,\,{65^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,{80^o}\\(C)\,{70^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,{50^o}\end{array}\)

Phương pháp:

- Trong một tam giác cân hai góc ở đáy bằng nhau.

- Tổng các góc của một tam giác bằng \(180^o\).

Lời giải:

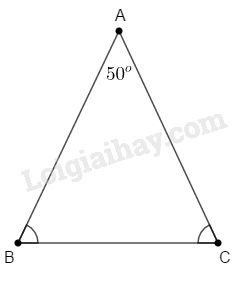
Xét \(\Delta ABC\) cân tại \(A\); \(\widehat A = {50^o}.\)

Theo tích chất tam giác cân thì \(\widehat B = \widehat C.\)

Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\) ta có:

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat A + \widehat B + \widehat B = {180^o}\\ \Rightarrow \widehat A + 2\widehat B = {180^o}\\ \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2}\\ \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^o} - {{50}^o}}}{2} = {65^o}\end{array}\)

Chọn A.

Câu 13.

Một tam giác cân có góc ở đáy bằng \({42^o}.\)  Góc ở đỉnh của tam giác cân đó bằng \(\begin{array}{l}(A)\,{69^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,{106^o}\\(C)\,{96^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,{48^o}\end{array}\)

Khoanh tròn vào chữ cái trước câu trả lời đúng.

Phương pháp:

- Trong một tam giác cân hai góc ở đáy bằng nhau.

- Tổng các góc của một tam giác bằng \(180^o\).

Lời giải:

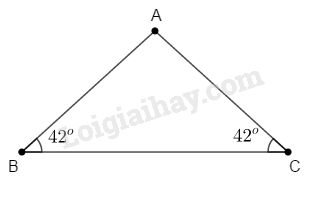
Xét \(\Delta ABC\) cân tại \(A\)

Theo tích chất tam giác cân thì \(\widehat B = \widehat C = {42^o}.\)

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right)\\ \Rightarrow \widehat A = {180^o} - \left( {{{42}^o} + {{42}^o}} \right)\\ \Rightarrow \widehat A = {96^o}\end{array}\)

Chọn C.

Câu 14.

Đúng ghi Đ, sai ghi S vào ô trống trong mỗi khẳng định sau:

a) Nếu mỗi tam giác vuông có một góc bằng \({45^o}\)  thì hai cạnh góc vuông bằng nhau.    \(\square\)

b) Nếu một tam giác có hai góc bằng \({60^o}\)  thì ba cạnh bằng nhau. \(\square\)

c) Góc ở đỉnh của tam giác cân không thể là góc tù. \(\square\)

d) Góc ở đáy của tam giác cân không thể là góc tù. \(\square\)

Phương pháp:

- Trong một tam giác cân hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau.

- Tổng các góc của một tam giác bằng \(180^o\).

- Trong tam giác vuông hai góc nhọn phụ nhau.

Lời giải:

a) Đ

Xét \(\Delta ABC\) có \(\widehat A = {90^o};\,\widehat B = {45^o}.\)

Suy ra  

Do đó \(\Delta ABC\) cân tại \(A\) nên hai cạnh góc vuông bằng nhau (tính chất tam giác cân)

b) Đ

Xét \(\Delta ABC\) có \(\widehat A = \widehat B = {60^o}.\)

\(\begin{array}{l}\widehat { \Rightarrow C} = {180^o} - \widehat A - \widehat B\\ \Rightarrow \widehat C = {180^o} - {60^o} - {60^o} = {60^o}.\end{array}\)

Do đó \(\Delta ABC\) là tam giác đều nên có ba cạnh bằng nhau.

c) S

Ví dụ: \(\Delta ABC\) có \(\widehat A = {120^o};\,\widehat B = \widehat C = {30^o}.\)

Do đó \(\Delta ABC\) cân tại \(A. \) (trong đó \(\widehat A\) là góc tù).

d) Đ

Phản chứng: Giả sử tồn tại \(\Delta ABC\) cân tại \(A\) có đáy là góc tù.

Suy ra \(\widehat B = \widehat C > {90^o}\) (do \(\widehat B;\widehat C\) tù).

Ta có: \(\widehat B + \widehat C > {90^o} + {90^o} = {180^o}\) (mâu thuẫn định lí tổng các góc của một tam giác).

Do đó không tồn tại tam giác cân có đáy là góc tù.