Bài 33 trang 133 Vở bài tập toán 7 tập 1

Đề bài

Cho góc \(xOy\) có số đo \(120^0\), điểm \(A\) thuộc tia phân giác của góc đó. Kẻ \(AB\) vuông góc với \(Ox\) (\(B\in Ox\)), kẻ \(AC\) vuông góc với \(Oy\) (\(C\in Oy\)). Tam giác \(ABC\) là tam giác gì ? Vì sao?

Lời giải chi tiết

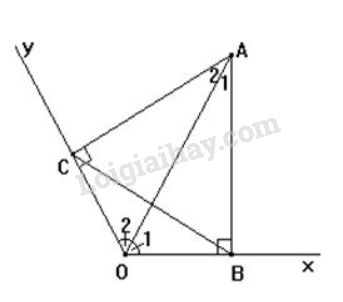
Các tam giác vuông \(AOB\) và \(AOC\) có:

cạnh huyền \(AO\) chung

\(\widehat{O_{1}}=\widehat{O_{2}}\) (Vì \(OA\) là tia phân giác của góc \(xOy\))

Do đó \(AOB=AOC\) (cạnh huyền-góc nhọn), suy ra \( AB=AC\) (hai cạnh tương ứng).

Các tam giác vuông \(AOB\) và \(AOC\) có \(\widehat {{O_1}} = \widehat {{O_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}\) nên \( \widehat {{A_1}} = \widehat {{A_2}} = {90^o} - {60^o} = {30^o}\), do đó \(\widehat {BAC} = \widehat {{A_1}} + \widehat {{A_2}} ={30^o}+{30^o}= {60^0}\)

Vây tam giác \(ABC\) là tam giác cân (vì \(AB=AC\)) lại có \(\widehat {BAC}= {60^0}\) nên là tam giác đều.