Phần câu hỏi bài 3 trang 94 Vở bài tập toán 9 tập 2

Câu 7.

Khoanh tròn vào chữ cái dưới hình chỉ góc nội tiếp ở hình 13:

Phương pháp giải:

Sử dụng định nghĩa góc nội tiếp : “Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó”.

Lời giải chi tiết:

Theo định nghĩa ta thấy chỉ có hình d thỏa mãn.

Chọn D.

Câu 8.

Trên đường tròn lần lượt đặt ba cung \(AB, BC, CA\) có số đo là \(x{\rm{ }} + {\rm{ }}{75^o},\) \({\rm{ }}2x{\rm{ }} + {\rm{ }}{25^o},\) \({\rm{ }}3x{\rm{ }}-{\rm{ }}{22^o}.\) Số đo của góc ACB là:

\(\left( A \right){\rm{ }}59^\circ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( B \right){\rm{ }}60^\circ \)

\(\left( C \right){\rm{ }}61^\circ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( D \right){\rm{ }}75^\circ \)

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Sử dụng “ số đo của cả đường tròn là \(360^\circ \)” để tìm \(x\), từ đó tính số đo cung \(AB.\)

Sử dụng số đo góc nội tiếp bằng nửa số đo cung bị chắn để tính góc \(ACB.\)

Lời giải chi tiết:

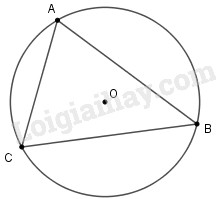
Ta có sđ\(\overparen{AB}\) + sđ\(\overparen{AC}\) + sđ\(\overparen{BC}\)

\( = 360^\circ\)

\( \Leftrightarrow x + 75^\circ\) \( + 2x + 25^\circ \) \(+ 3x - 22^\circ  \) \(= 360^\circ \)

\( \Leftrightarrow 6x = 282^\circ  \Leftrightarrow x = 47^\circ .\)

Suy ra sđ\(\overparen{AB}\) \( = x + 75^\circ  \)\(= 47^\circ  + 75^\circ\)\(  = 122^\circ \)

Nhận thấy \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \dfrac{1}{2}\)sđ\(\overparen{AB}\)

\( = \dfrac{1}{2}.122^\circ\)\(  = 61^\circ \).

Chọn C.