Bài 14 trang 96 Vở bài tập toán 9 tập 2
Giải bài 14 trang 96 VBT toán 9 tập 2. Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C...
Đề bài
Trên đường tròn \((O)\) đường kính \(AB\), lấy điểm \(M\) (khác \(A\) và \(B\)). vẽ tiếp tuyến của \((O)\) tại \(A\). Đừờng thẳng \(BM\) cắt tiếp tuyến đó tại \(C\). Chứng minh rằng ta luôn có \(M{A^2} = {\rm{ }}MB.MC\)
Phương pháp giải - Xem chi tiết
+ Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Chứng minh \(\Delta {\rm M}{\rm A}{\rm B}\) đồng dạng với \(\Delta MCA\) từ đó suy ra tỉ lệ cạnh để có đẳng thức cần chứng minh.
Lời giải chi tiết
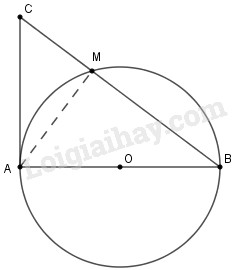
Nối \(AM\)
Xét \(\Delta AMB\) và \(\Delta AMC.\)
Ta có \(\widehat M = 90^\circ \) vì góc nội tiếp chắn nửa đường tròn
Và \(\widehat {MAC} = \widehat {MBA}\) vì \(\widehat {MBA} + \widehat {MAB} = 90^\circ \) (vì tam giác \(MAB\) vuông tại \(M\) ) và \(\widehat {MAB} + \widehat {MAC} = 90^\circ \) (do \(\widehat {BAC} = 90^\circ \))
Hai tam giác vuông có góc nhọn bằng nhau \( \Rightarrow \) \(\Delta MAB\) \( \backsim \) \(\Delta MCA\) nên ta có :
\(\dfrac{{MA}}{{MC}} = \dfrac{{MB}}{{MA}} \Rightarrow M{A^2} = MB.MC\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 14 trang 96 Vở bài tập toán 9 tập 2 timdapan.com"