Phần câu hỏi bài 1 trang 131, 132 Vở bài tập toán 9 tập 2

Câu 1

Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ. Biết rằng BC = 3 cm; AB = 6 cm. Diện tích xung quanh của một hình trụ bằng:

(A) \(18\pi \,\,c{m^2}\)               (B) \(26\pi \,\,c{m^2}\)

(C \(36\pi \,\,c{m^2}\)                (D) \(38\pi \,\,c{m^2}\) 

Phương pháp giải:

Diện tích xung quanh của hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \({S_{xq}} = 2\pi rh\)

Lời giải chi tiết:

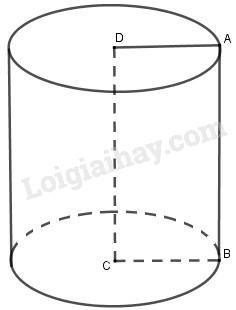
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ có bán kính đáy \(R = BC = 3cm\) và chiều cao \(DC = AB = 6cm\) nên diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi Rh = 2\pi .3.6 = 36\pi \left( {c{m^2}} \right)\)

Chọn C.

Câu 2

Một hình trụ có đường kính đáy d là 12,6 cm, diện tích xung quanh bằng 333,5 cm². Khi đó, chiều cao h của hình trụ xấp xỉ là (lấy \(\pi  = 3,14)\):

(A) 7,9 cm                               (B) 8,2 cm

(C 8,4 cm                                (D) 9,2 cm

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Tính bán kính đáy \(r = \dfrac{d}{2}\)

Từ công thức tính diện tích xung quanh của hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \({S_{xq}} = 2\pi rh\) ta tính được chiều cao \(h.\)

Lời giải chi tiết:

Bán kính đáy hình trụ là \(r = \dfrac{d}{2} = \dfrac{{12,6}}{2} = 6,3cm\)

Gọi chiều cao hình trụ là \(h\) thì diện tích xung quang hình trụ là \(S = 2\pi rh = 2\pi .6,3.h = 12,6\pi .h\)

Từ đề bài ta có \(12,6\pi h = 333,5 \Leftrightarrow h = \dfrac{{333,5}}{{12,6\pi }}\)\( \approx 8,4cm\)

Chọn C.

Câu 3

Một hình trụ có thể tích 147,4 cm², chiều cao 7,5 cm. Nếu làm tròn đến chữ số thập phân thứ hai thì bán kính đáy r của hình trụ xấp xỉ là (lấy \(\pi  = 3,14\) ):

(A) 2,2 cm                               (B) 2,5 cm

(C 2,8 cm                                (D) 3,2 cm

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Thể tích hình trụ \(V = \pi {r^2}h\) với \(r\) là bán kính đáy và \(h\) là chiều cao hình trụ.

Lời giải chi tiết:

Gọi \(r\left( {r > 0} \right)\) là bán kính đáy của hình trụ

Thể tích hình trụ là \(V = \pi {r^2}h = \pi {r^2}.7,5\)

Theo đề bài ta có \(7,5\pi {r^2} = 147,2 \Leftrightarrow {r^2} = \dfrac{{147,2}}{{7,5\pi }}\)\( \Rightarrow r = \sqrt {\dfrac{{147,2}}{{7,5\pi }}}  \approx 2,5cm\)

Chọn B.